An aperture (i.e., slit or hole) of size a illuminated by a parallel beam sends diffracted light into an angle of approximately ≈ λ/a. This is the angular size of the bright central maximum. In travelling a distance z, the diffracted beam therefore acquires a width zλ/a due to diffraction. It is interesting to ask at what value of z the spreading due to diffraction becomes comparable to the size a of the aperture. We thus approximately equate zλ/a with a. This gives the distance beyond which divergence of the beam of width a becomes significant. Therefore,
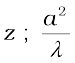(10.31)
We define a quantity zF called the Fresnel distance by the following equation
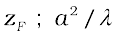
Equation (10.31) shows that for distances much smaller than zF , the spreading due to diffraction is smaller compared to the size of the beam. It becomes comparable when the distance is approximately zF. For distances much greater than zF, the spreading due to diffraction dominates over that due to ray optics (i.e., the size a of the aperture). Equation (10.31) also shows that ray optics is valid in the limit of wavelength tending to zero.
Example 10.7 For what distance is ray optics a good approximation when the aperture is 3 mm wide and the wavelength is 500 nm?
Solution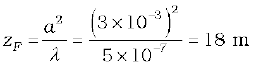 
This example shows that even with a small aperture, diffraction spreading can be neglected for rays many metres in length. Thus, ray optics is valid in many common situations.
© 2025 GoodEd Technologies Pvt. Ltd.
