We should mention here that one should be careful in constructing the wavefronts if the source (or the observer) is moving. For example, if there is no medium and the source moves away from the observer, then later wavefronts have to travel a greater distance to reach the observer and hence take a longer time. The time taken between the arrival of two successive wavefronts is hence longer at the observer than it is at the source. Thus, when the source moves away from the observer the frequency as measured by the source will be smaller. This is known as the Doppler effect. Astronomers call the increase in wavelength due to doppler effect as red shift since a wavelength in the middle of the visible region of the spectrum moves towards the red end of the spectrum. When waves are received from a source moving towards the observer, there is an apparent decrease in wavelength, this is referred to as blue shift.
You have already encountered Doppler effect for sound waves in Chapter 15 of Class XI textbook. For velocities small compared to the speed of light, we can use the same formulae which we use for sound waves. The fractional change in frequency ∆ν/ν is given by –vradial/c, where vradial is the component of the source velocity along the line joining the observer to the source relative to the observer; vradial is considered positive when the source moves away from the observer. Thus, the Doppler shift can be expressed as:
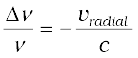(10.9)
The formula given above is valid only when the speed of the source is small compared to that of light. A more accurate formula for the Doppler effect which is valid even when the speeds are close to that of light, requires the use of Einstein’s special theory of relativity. The Doppler effect for light is very important in astronomy. It is the basis for the measurements of the radial velocities of distant galaxies.
Example 10.1 What speed should a galaxy move with respect to us so that the sodium line at 589.0 nm is observed at 589.6 nm?
Solution Since νλ = c,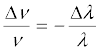 
(for small changes in ν and λ). For
∆λ = 589.6 – 589.0 = + 0.6 nm
we get [using Eq. (10.9)]
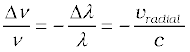
or, vradial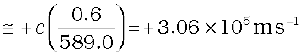 
= 306 km/s
Therefore, the galaxy is moving away from us.
Example 10.2
(a) When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency. Explain why?
(b) When light travels from a rarer to a denser medium, the speed decreases. Does the reduction in speed imply a reduction in the energy carried by the light wave?
(c) In the wave picture of light, intensity of light is determined by the square of the amplitude of the wave. What determines the intensity of light in the photon picture of light.
Solution
(a) Reflection and refraction arise through interaction of incident light with the atomic constituents of matter. Atoms may be viewed as
oscillators, which take up the frequency of the external agency (light) causing forced oscillations. The frequency of light emitted by a charged oscillator equals its frequency of oscillation. Thus, the frequency of scattered light equals the frequency of incident light.
(b) No. Energy carried by a wave depends on the amplitude of the wave, not on the speed of wave propagation.
(c) For a given frequency, intensity of light in the photon picture is determined by the number of photons crossing an unit area per unit time.
