We have so far considered refraction at a plane interface. We shall now consider refraction at a spherical interface between two transparent media. An infinitesimal part of a spherical surface can be regarded as planar and the same laws of refraction can be applied at every point on the surface. Just as for reflection by a spherical mirror, the normal at the point of incidence is perpendicular to the tangent plane to the spherical surface at that point and, therefore, passes through its centre of curvature. We first consider refraction by a single spherical surface and follow it by thin lenses. A thin lens is a transparent optical medium bounded by two surfaces; at least one of which should be spherical. Applying the formula for image formation by a single spherical surface successively at the two surfaces of a lens, we shall obtain the lens maker’s formula and then the lens formula.
Figure 9.17 shows the geometry of formation of image I of an object O on the principal axis of a spherical surface with centre of curvature C, and radius of curvature R. The rays are incident from a medium of refractive index n1, to another of refractive index n2. As before, we take the aperture (or the lateral size) of the surface to be small compared to other distances involved, so that small angle approximation can be made. In particular, NM will be taken to be nearly equal to the length of the perpendicular from the point N on the principal axis. We have, for small angles,
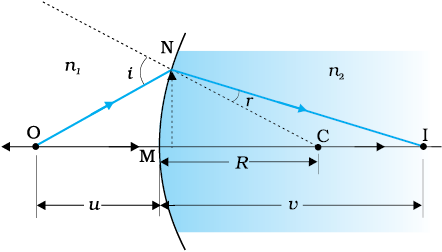
tan ∠NOM = 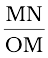
tan ∠NCM = 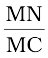
tan ∠NIM = 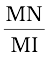
Now, for ∆NOC, i is the exterior angle. Therefore, i = ∠NOM + ∠NCM
i = 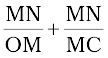 (9.13)
(9.13)
Similarly,
r = ∠NCM – ∠NIM
i.e., r = 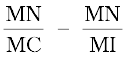 (9.14)
(9.14)
Now, by Snell’s law
Substituting i and r from Eqs. (9.13) and (9.14), we get
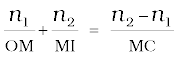 (9.15)
(9.15)
Here, OM, MI and MC represent magnitudes of distances. Applying the Cartesian sign convention,
OM = –u, MI = +v, MC = +R
Substituting these in Eq. (9.15), we get
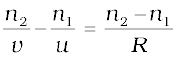 (9.16)
(9.16)
Equation (9.16) gives us a relation between object and image distance in terms of refractive index of the medium and the radius of curvature of the curved spherical surface. It holds for any curved spherical surface.
Example 9.6 Light from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed?
Solution
We use the relation given by Eq. (9.16). Here
u = – 100 cm, v = ?, R = + 20 cm, n1 = 1, and n2 = 1.5.
We then have
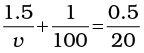
or v = +100 cm
The image is formed at a distance of 100 cm from the glass surface, in the direction of incident light.