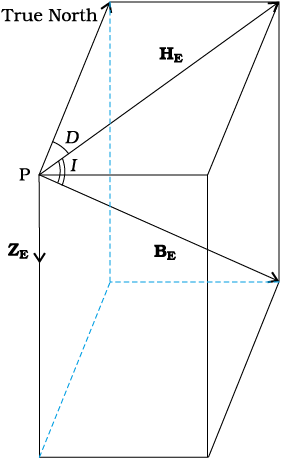
Consider a point on the earth’s surface. At such a point, the direction of the longitude circle determines the geographic north-south direction, the line of longitude towards the north pole being the direction of true north. The vertical plane containing the longitude circle and the axis of rotation of the earth is called the geographic meridian. In a similar way, one can define magnetic meridian of a place as the vertical plane which passes through the imaginary line joining the magnetic north and the south poles. This plane would intersect the surface of the earth in a longitude like circle. A magnetic needle, which is free to swing horizontally, would then lie in the magnetic meridian and the north pole of the needle would point towards the magnetic north pole. Since the line joining the magnetic poles is titled with respect to the geographic axis of the earth, the magnetic meridian at a point makes angle with the geographic meridian. This, then, is the angle between the true geographic north and the north shown by a compass needle. This angle is called the magnetic declination or simply declination (Fig. 5.9).
The declination is greater at higher latitudes and smaller near the equator. The declination in India is small, it being 0°41′ E at Delhi and 0°58′ W at Mumbai. Thus, at both these places a magnetic needle shows the true north quite accurately.
Figure 5.9 A magnetic needle free to move in horizontal plane, points toward the magnetic north-south direction.
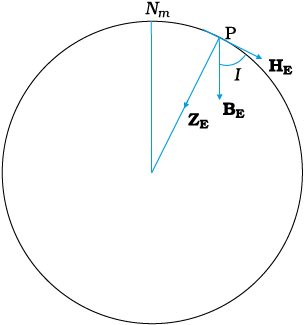
There is one more quantity of interest. If a magnetic needle is perfectly balanced about a horizontal axis so that it can swing in a plane of the magnetic meridian, the needle would make an angle with the horizontal (Fig. 5.10). This is known as the angle of dip (also known as inclination). Thus, dip is the angle that the total magnetic field BE of the earth makes with the surface of the earth. Figure 5.11 shows the magnetic meridian plane at a point P on the surface of the earth. The plane is a section through the earth. The total magnetic field at P can be resolved into a horizontal component HE and a vertical component ZE. The angle that BE makes with HE is the angle of dip, I.
In most of the northern hemisphere, the north pole of the dip needle tilts downwards. Likewise in most of the southern hemisphere, the south pole of the dip needle tilts downwards.
To describe the magnetic field of the earth at a point on its surface, we need to specify three quantities, viz., the declination D, the angle of dip or the inclination I and the horizontal component of the earth’s field HE . These are known as the element of the earth’s magnetic field.
Representing the verticle component by ZE, we have
Figure 5.10 The circle is a section through the earth containing the magnetic meridian. The angle between BE and the horizontal component HE is the angle of dip.
ZE = BE sinI [5.10(a)]
HE = BE cosI [5.10(b)]
which gives,
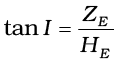[5.10(c)]
© 2025 GoodEd Technologies Pvt. Ltd.
