We know that accurate measurement of an unknown resistance can be performed on a Wheatstone bridge. However, for measuring the resistance of an ionic solution we face two problems. Firstly, passing direct current (DC) changes the composition of the solution. Secondly, a solution cannot be connected to the bridge like a metallic wire or other solid conductor. The first difficulty is resolved by using an alternating current (AC) source of power. The second problem is solved by using a specially designed vessel called conductivity cell. It is available in several designs and two simple ones are shown in Fig. 3.4.
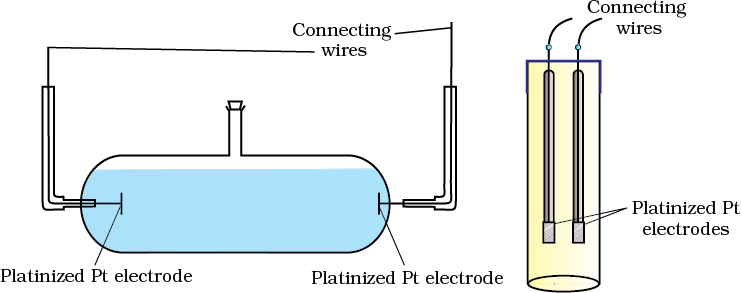
Fig. 3.4 Two different types of conductivity cells.
Basically it consists of two platinum electrodes coated with platinum black (finely divided metallic Pt is deposited on the electrodes electrochemically). These have area of cross section equal to ‘A’ and are separated by distance ‘l’. Therefore, solution confined between these electrodes is a column of length l and area of cross section A. The resistance of such a column of solution is then given by the equation:
R = ρ 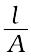 =
= 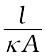 (3.17)
(3.17)
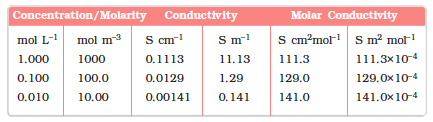
The quantity l / A is called cell constant denoted by the symbol, G*. It depends on the distance between the electrodes and their area of cross-section and has the dimension of length–1 and can be calculated if we know l and A. Measurement of l and A is not only inconvenient but also unreliable. The cell constant is usually determined by measuring the resistance of the cell containing a solution whose conductivity is already known. For this purpose, we generally use KCl solutions whose conductivity is known accurately at various concentrations (Table 3.3) and at different temperatures. The cell constant, G*, is then given by the equation:
G* = 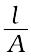 = R κ (3.18)
= R κ (3.18)
Table 3.3: Conductivity and Molar conductivity of KCl solutions at 298.15K
Once the cell constant is determined, we can use it for measuring the resistance or conductivity of any solution. The set up for the measurement of the resistance is shown in Fig. 3.5.
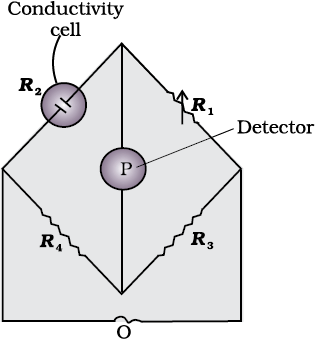
It consists of two resistances R3 and R4, a variable resistance R1 and the conductivity cell having the unknown resistance R2. The Wheatstone bridge is fed by an oscillator O (a source of a.c. power in the audio frequency range 550 to 5000 cycles per second). P is a suitable detector (a headphone or other electronic device) and the bridge is balanced when no current passes through the detector. Under these conditions:
Unknown resistance R2 = 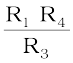 (3.19)
(3.19)
These days, inexpensive conductivity meters are available which can directly read the conductance or resistance of the solution in the conductivity cell. Once the cell constant and the resistance of the solution in the cell is determined, the conductivity of the solution is given by the equation:
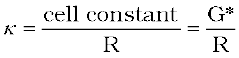 (3.20)
(3.20)
The conductivity of solutions of different electrolytes in the same solvent and at a given temperature differs due to charge and size of the ions in which they dissociate, the concentration of ions or ease with which the ions move under a potential gradient. It, therefore, becomes necessary to define a physically more meaningful quantity called molar conductivity denoted by the symbol Λm (Greek, lambda). It is related to the conductivity of the solution by the equation:
Molar conductivity = Λm = 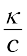 (3.21)
(3.21)
In the above equation, if κ is expressed in S m–1 and the concentration, c in mol m–3 then the units of Λm are in S m2 mol–1. It may be noted that:
1 mol m–3 = 1000(L/m3) × molarity (mol/L), and hence
Λm(S cm2 mol–1) = 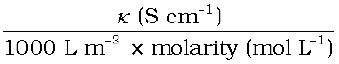
If we use S cm–1 as the units for κ and mol cm–3, the units of concentration, then the units for Λm are S cm2 mol–1. It can be calculated by using the equation:
Λm (S cm2 mol–1) = 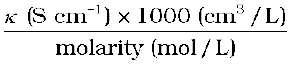
Both type of units are used in literature and are related to each other by the equations:
1 S m2mol–1 = 104 S cm2mol–1 or
1 S cm2mol–1 = 10–4 S m2mol–1.
Example 3.4
Resistance of a conductivity cell filled with 0.1 mol L–1 KCl solution is 100 Ω . If the resistance of the same cell when filled with 0.02 mol L–1 KCl solution is 520 Ω , calculate the conductivity and molar conductivity of 0.02 mol L–1 KCl solution. The conductivity of 0.1 mol L–1 KCl solution is 1.29 S/m.
Solution
The cell constant is given by the equation:
Cell constant = G* = conductivity × resistance
= 1.29 S/m × 100 Ω = 129 m–1 = 1.29 cm–1
Conductivity of 0.02 mol L–1 KCl solution = cell constant / resistance
= 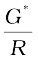 =
= 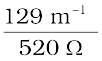 = 0.248 S m–1
= 0.248 S m–1
Concentration = 0.02 mol L–1
= 1000 × 0.02 mol m–3 = 20 mol m–3
Molar conductivity = 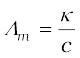
= 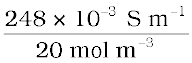 = 124 × 10–4 S m2mol–1
= 124 × 10–4 S m2mol–1
Alternatively, κ = 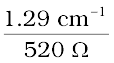 = 0.248 × 10–2 S cm–1
= 0.248 × 10–2 S cm–1
and Λm = κ × 1000 cm3 L–1 molarity–1
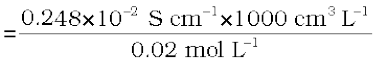
= 124 S cm2 mol–1
Example 3.5
The electrical resistance of a column of 0.05 mol L–1 NaOH solution of diameter 1 cm and length 50 cm is 5.55 × 103 ohm. Calculate its resistivity, conductivity and molar conductivity.
Solution
A = π r2 = 3.14 × 0.52 cm2 = 0.785 cm2 = 0.785 × 10–4 m2
l = 50 cm = 0.5 m
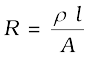 or
or 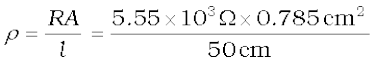 =87.135 Ω cm
=87.135 Ω cm
Conductivity = 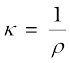 =
= 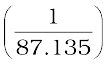 S cm–1
S cm–1
= 0.01148 S cm–1
Molar conductivity, 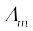 =
= 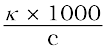 cm3 L–1
cm3 L–1
= 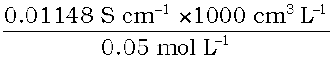
= 229.6 S cm2 mol–1
If we want to calculate the values of different quantities in terms of ‘m’ instead of ‘cm’,
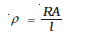
= 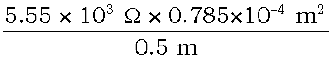 = 87.135 ×10–2 Ω m
= 87.135 ×10–2 Ω m
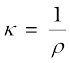 =
= 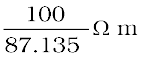 = 1.148S m–1
= 1.148S m–1
and 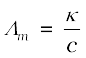 =
= 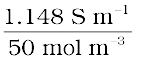 = 229.6 × 10–4 S m2 mol–1.
= 229.6 × 10–4 S m2 mol–1.