13.6.4 Specific Heat Capacity of Solids

 We can use the law of equipartition of energy to determine specific heats of solids. Consider a solid of N atoms, each vibrating about its mean position. An oscillation in one dimension has average energy of 2 × ½ k_BT = k_BT . In three dimensions, the average energy is 3k_BT. For a mole of solid, N = NA, and the total energy is

U = 3 k_BT × N_A = 3 RT

Now at constant pressure ∆Q = ∆U + P∆V 

= ∆U, since for a solid ∆V is negligible. Hence,

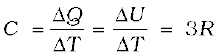(13.37)

Table 13.3 Specific Heat Capacity of some solids at room temperature and atmospheric pressure

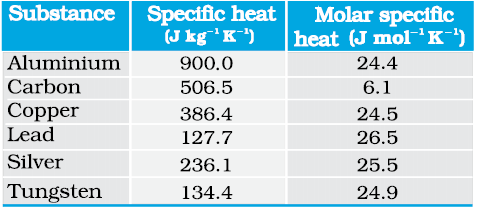
As Table 13.3 shows the prediction generally agrees with experimental values at ordinary temperature (Carbon is an exception).

13.6.5 Specific Heat Capacity of Water

 We treat water like a solid. For each atom average energy is 3k_BT. Water molecule has three atoms, two hydrogen and one oxygen. So it has

U = 3 × 3 k_BT × N_A = 9 RT

and C = ∆Q/ ∆T =∆ U / ∆T = 9R .

This is the value observed and the agreement is very good. In the calorie, gram, degree units, water is defined to have unit specific heat. As 1 calorie = 4.179 joules and one mole of water is 18 grams, the heat capacity per mole is ~ 75 J mol^-1 K^-1 ~ 9R. However with more complex molecules like alcohol or acetone the arguments, based on degrees of freedom, become more complicated.

Lastly, we should note an important aspect of the predictions of specific heats, based on the classical law of equipartition of energy. The predicted specific heats are independent of temperature. As we go to low temperatures, however, there is a marked departure from this prediction. Specific heats of all substances approach zero as T -> 0. This is related to the fact that degrees of freedom get frozen and ineffective at low temperatures. According to classical physics, degrees of freedom must remain unchanged at all times. The behaviour of specific heats at low temperatures shows the inadequacy of classical physics and can be explained only by invoking quantum considerations, as was first shown by Einstein. Quantum mechanics requires a minimum, non-zero amount of energy before a degree of freedom comes into play. This is also the reason why vibrational degrees of freedom come into play only in some cases.