7.8 Equilibrium of a rigid Body

We are now going to concentrate on the motion of rigid bodies rather than on the motion of general systems of particles.

We shall recapitulate what effect the external forces have on a rigid body. (Henceforth we shall omit the adjective ‘external’ because unless stated otherwise, we shall deal with only external forces and torques.) The forces change the translational state of the motion of the rigid body, i.e. they change its total linear momentum in accordance with Eq. (7.17). But this is not the only effect the forces have. The total torque on the body may not vanish. Such a torque changes the rotational state of motion of the rigid body, i.e. it changes the total angular momentum of the body in accordance with Eq. (7.28 b).

A rigid body is said to be in mechanical equilibrium, if both its linear momentum and angular momentum are not changing with time, or equivalently, the body has neither linear acceleration nor angular acceleration. This means

(1) the total force, i.e. the vector sum of the forces, on the rigid body is zero;

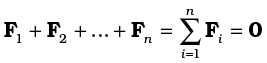
If the total force on the body is zero, then the total linear momentum of the body does not change with time. Eq. (7.30a) gives the condition for the translational equilibrium of the body.

(2) The total torque, i.e. the vector sum of the torques on the rigid body is zero,

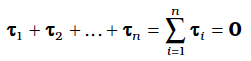
If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time. Eq. (7.30 b) gives the condition for the rotational equilibrium of the body.

One may raise a question, whether the rotational equilibrium condition [Eq. 7.30(b)] remains valid, if the origin with respect to which the torques are taken is shifted. One can show that if the translational equilibrium condition [Eq. 7.30(a)] holds for a rigid body, then such a shift of origin does not matter, i.e. the rotational equilibrium condition is independent of the location of the origin about which the torques are taken. Example 7.7 gives a proof of this result in a special case of a couple, i.e. two forces acting on a rigid body in translational equilibrium. The generalisation of this result to n forces is left as an exercise.

Eq. (7.30a) and Eq. (7.30b), both, are vector equations. They are equivalent to three scalar equations each. Eq. (7.30a) corresponds to

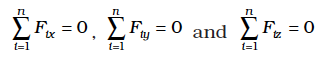
where Fix, Fiy and Fiz are respectively the x, y and z components of the forces Fi. Similarly, Eq. (7.30b) is equivalent to three scalar equations

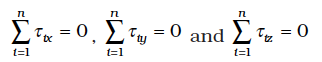
where τix, τiy and τiz are respectively the x, y and z components of the torque τi .

Eq. (7.31a) and (7.31b) give six independent conditions to be satisfied for mechanical equilibrium of a rigid body. In a number of problems all the forces acting on the body are coplanar. Then we need only three conditions to be satisfied for mechanical equilibrium. Two of these conditions correspond to translational equilibrium; the sum of the components of the forces along any two perpendicular axes in the plane must be zero. The third condition corresponds to rotational equilibrium. The sum of the components of the torques along any axis perpendicular to the plane of the forces must be zero.

The conditions of equilibrium of a rigid body may be compared with those for a particle, which we considered in earlier chapters. Since consideration of rotational motion does not apply to a particle, only the conditions for translational equilibrium (Eq. 7.30 a) apply to a particle. Thus, for equilibrium of a particle the vector sum of all the forces on it must be zero. Since all these forces act on the single particle, they must be concurrent. Equilibrium under concurrent forces was discussed in the earlier chapters. 

A body may be in partial equilibrium, i.e., it may be in translational equilibrium and not in rotational equilibrium, or it may be in rotational equilibrium and not in translational equilibrium. 

Consider a light (i.e. of negligible mass) rod (AB) as shown in Fig. 7.20(a). At the two ends (A and B) of which two parallel forces, both equal in magnitude and acting along same direction are applied perpendicular to the rod.

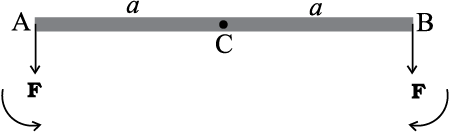
Fig. 7.20 (a)

Let C be the midpoint of AB, CA = CB = a. the moment of the forces at A and B will both be equal in magnitude (aF), but opposite in sense as shown. The net moment on the rod will be zero. The system will be in rotational equilibrium, but it will not be in translational equilibrium;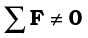

Fig. 7.20 (b)

The force at B in Fig. 7.20(a) is reversed in Fig. 7.20(b). Thus, we have the same rod with two forces of equal magnitude but acting in opposite diretions applied perpendicular to the rod, one at end A and the other at end B. Here the moments of both the forces are equal, but they are not opposite; they act in the same sense and cause anticlockwise rotation of the rod. The total force on the body is zero; so the body is in translational equilibrium; but it is not in rotational equilibrium. Although the rod is not fixed in any way, it undergoes pure rotation (i.e. rotation without translation).

A pair of forces of equal magnitude but acting in opposite directions with different lines of action is known as a couple or torque. A couple produces rotation without translation. 

When we open the lid of a bottle by turning it, our fingers are applying a couple to the lid [Fig. 7.21(a)]. Another known example is a compass needle in the earth’s magnetic field as shown in the Fig. 7.21(b). The earth’s magnetic field exerts equal forces on the north and south poles. The force on the North Pole is towards the north, and the force on the South Pole is toward the south. Except when the needle points in the north-south direction; the two forces do not have the same line of action. Thus there is a couple acting on the needle due to the earth’s magnetic field.

Fig. 7.21(a) Our fingers apply a couple to turn the lid.

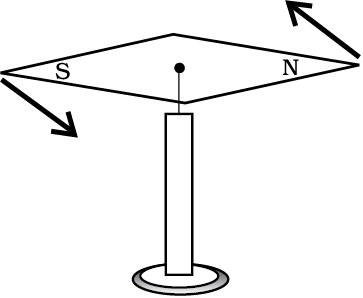
Fig. 7.21(b) The Earth’s magnetic field exerts equal and opposite forces on the poles of a compass needle. These two forces form a couple.

Answer

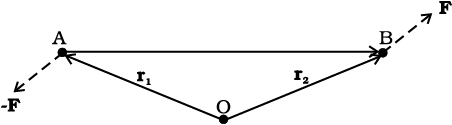
Fig. 7.22

Consider a couple as shown in Fig. 7.22 acting on a rigid body. The forces F and -F act respectively at points B and A. These points have position vectors r1 and r2 with respect to origin O. Let us take the moments of the forces about the origin.

The moment of the couple = sum of the moments of the two forces making the couple

= r1 × (–F) + r2 × F

= r2 × F – r1 × F

= (r2–r1) × F

But r1 + AB = r2, and hence AB = r2 – r1.

The moment of the couple, therefore, is AB × F.

Clearly this is independent of the origin, the point about which we took the moments of the forces.