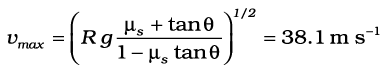5.10 Circular motion

We have seen in Chapter 4 that acceleration of a body moving in a circle of radius R with uniform speed v is v2/R directed towards the centre. According to the second law, the force fc providing this acceleration is :

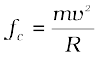
where m is the mass of the body. This force directed forwards the centre is called the centripetal force. For a stone rotated in a circle by a string, the centripetal force is provided by the tension in the string. The centripetal force for motion of a planet around the sun is the gravitational force on the planet due to the sun. For a car taking a circular turn on a horizontal road, the centripetal force is the force of friction.

The circular motion of a car on a flat and banked road give interesting application of the laws of motion.

Motion of a car on a level road

Three forces act on the car (Fig. 5.14(a):

(i) The weight of the car, mg

(ii) Normal reaction, N

(iii) Frictional force, f

As there is no acceleration in the vertical direction

N – mg = 0

N = mg                                                                                             (5.17)

The centripetal force required for circular motion is along the surface of the road, and is provided by the component of the contact force between road and the car tyres along the surface. This by definition is the frictional force. Note that it is the static friction that provides the centripetal acceleration. Static friction opposes the impending motion of the car moving away from the circle. Using equation (5.14) & (5.16) we get the result

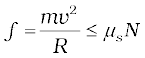
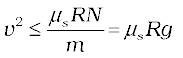[ ∵N = mg]

which is independent of the mass of the car.

This shows that for a given value of µs and R, there is a maximum speed of circular motion of the car possible, namely

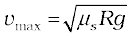
Motion of a car on a banked road

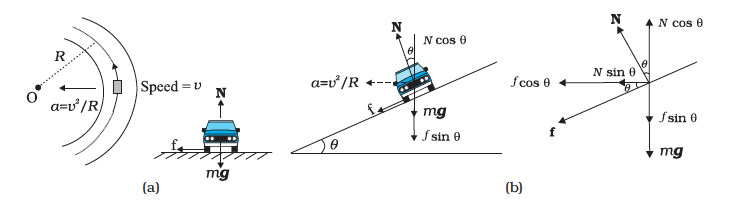
Fig. 5.14 Circular motion of a car on (a) a level road, (b) a banked road.

We can reduce the contribution of friction to the circular motion of the car if the road is banked (Fig. 5.14(b)). Since there is no acceleration along the vertical direction, the net force along this direction must be zero. Hence,

N cos θ  = mg + f sin θ                                                                    (5.19a)

The centripetal force is provided by the horizontal components of N and f.

N sin θ + f cos θ =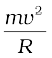

But f ≤ µsN

Thus to obtain vmax we put

f = µsN.

Then Eqs. (5.19a) and (5.19b) become

N cos θ = mg + µsN sin θ                                                                                              (5.20a)

N sin θ + µsN cos θ= mv2/R                                                                                         (5.20b)

From Eq. (5.20a), we obtain

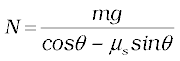
Substituting value of N in Eq. (5.20b), we get

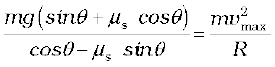
or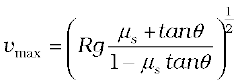

Comparing this with Eq. (5.18) we see that maximum possible speed of a car on a banked road is greater than that on a flat road.

For µs = 0 in Eq. (5.21 ),

vo = ( R g tan θ ) ½                                                                                                          (5.22)

At this speed, frictional force is not needed at all to provide the necessary centripetal force. Driving at this speed on a banked road will cause little wear and tear of the tyres. The same equation also tells you that for v < vo, frictional force will be up the slope and that a car can be parked only if tan θ ≤ µs.

Answer On an unbanked road, frictional force alone can provide the centripetal force needed to keep the cyclist moving on a circular turn without slipping. If the speed is too large, or if the turn is too sharp (i.e. of too small a radius) or both, the frictional force is not sufficient to provide the necessary centripetal force, and the cyclist slips. The condition for the cyclist not to slip is given by Eq. (5.18) :

v2 ≤ µs R g

Now, R = 3 m, g = 9.8 m s-2, µs = 0.1. That is, µs R g = 2.94 m2 s-2. v = 18 km/h = 5 m s-1; i.e., v2 = 25 m2 s-2. The condition is not obeyed. The cyclist will slip while taking the circular turn.

Answer On a banked road, the horizontal component of the normal force and the frictional force contribute to provide centripetal force to keep the car moving on a circular turn without slipping. At the optimum speed, the normal reaction’s component is enough to provide the needed centripetal force, and the frictional force is not needed. The optimum speed vo is given by Eq. (5.22):

vo = (R g tan θ)1/2

Here R = 300 m, θ = 15°, g = 9.8 m s-2; we have

vo = 28.1 m s-1.

The maximum permissible speed vmax is given by Eq. (5.21):