5.9.1 Friction

Let us return to the example of a body of mass m at rest on a horizontal table. The force of gravity (mg) is cancelled by the normal reaction force (N) of the table. Now suppose a force F is applied horizontally to the body. We know from experience that a small applied force may not be enough to move the body. But if the applied force F were the only external force on the body, it must move with acceleration F/m, however small. Clearly, the body remains at rest because some other force comes into play in the horizontal direction and opposes the applied force F, resulting in zero net force on the body. This force fs parallel to the surface of the body in contact with the table is known as frictional force, or simply friction (Fig. 5.10(a)). The subscript stands for static friction to distinguish it from kinetic friction fk that we consider later (Fig. 5.10(b)). Note that static friction does not exist by itself. When there is no applied force, there is no static friction. It comes into play the moment there is an applied force. As the applied force F increases, fs also increases, remaining equal and opposite to the applied force (up to a certain limit), keeping the body at rest. Hence, it is called static friction. Static friction opposes impending motion. The term impending motion means motion that would take place (but does not actually take place) under the applied force, if friction were absent.

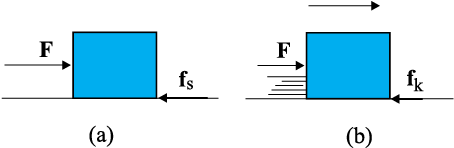
Fig. 5.10 Static and sliding friction: (a) Impending motion of the body is opposed by static friction. When external force exceeds the maximum limit of static friction, the body begins to move. (b) Once the body is in motion, it is subject to sliding or kinetic friction which opposes relative motion between the two surfaces in contact. Kinetic friction is usually less than the maximum value of static friction.

We know from experience that as the applied force exceeds a certain limit, the body begins to move. It is found experimentally that the limiting value of static friction 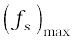is independent of the area of contact and varies with the normal force(N) approximately as :

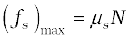
where µs is a constant of proportionality depending only on the nature of the surfaces in contact. The constant µs is called the coefficient of static friction. The law of static friction may thus be written as

fs ≤ µs N                                                                                                                           (5.14)

If the applied force F exceeds 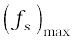the body begins to slide on the surface. It is found experimentally that when relative motion has started, the frictional force decreases from the static maximum value 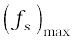. Frictional force that opposes relative motion between surfaces in contact is called kinetic or sliding friction and is denoted by fk . Kinetic friction, like static friction, is found to be independent of the area of contact. Further, it is nearly independent of the velocity. It satisfies a law similar to that for static friction:

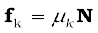
where µk′ the coefficient of kinetic friction, depends only on the surfaces in contact. As mentioned above, experiments show that µk is less than µs. When relative motion has begun, the acceleration of the body according to the second law is ( F – fk )/m. For a body moving with constant velocity, F = fk. If the applied force on the body is removed, its acceleration is – fk /m and it eventually comes to a stop.

The laws of friction given above do not have the status of fundamental laws like those for gravitational, electric and magnetic forces. They are empirical relations that are only
approximately true. Yet they are very useful in practical calculations in mechanics.

Thus, when two bodies are in contact, each experiences a contact force by the other. Friction, by definition, is the component of the contact force parallel to the surfaces in contact, which opposes impending or actual relative motion between the two surfaces. Note that it is not motion, but relative motion that the frictional force opposes. Consider a box lying in the compartment of a train that is accelerating. If the box is stationary relative to the train, it is in fact accelerating along with the train. What forces cause the acceleration of the box? Clearly, the only conceivable force in the horizontal direction is the force of friction. If there were no friction, the floor of the train would slip by and the box would remain at its initial position due to inertia (and hit the back side of the train). This impending relative motion is opposed by the static friction fs. Static friction provides the same acceleration to the box as that of the train, keeping it stationary relative to the train.

Answer Since the acceleration of the box is due to the static friction,

ma = fs ≤ µs N = µs m g

i.e. a ≤ µs g

∴ amax = µs g = 0.15 x 10 m s–2

= 1.5 m s–2

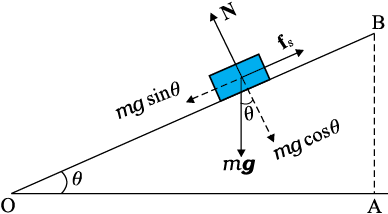
Fig. 5.11

Answer The forces acting on a block of mass m at rest on an inclined plane are (i) the weight mg acting vertically downwards (ii) the normal force N of the plane on the block, and (iii) the static frictional force fs opposing the impending motion. In equilibrium, the resultant of these forces must be zero. Resolving the weight mg along the two directions shown, we have

m g sin θ = fs , m g cos θ = N

As θ increases, the self-adjusting frictional force fs increases until at θ = θmax, fs achieves its maximum value, 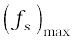= µs N.

Therefore,

tan θmax = µs or θmax = tan–1 µs

When θ becomes just a little more than θmax , there is a small net force on the block and it begins to slide. Note that θmax depends only on µs and is independent of the mass of the block.

For θmax = 15°,

µs = tan 15°

= 0.27

Fig. 5.12

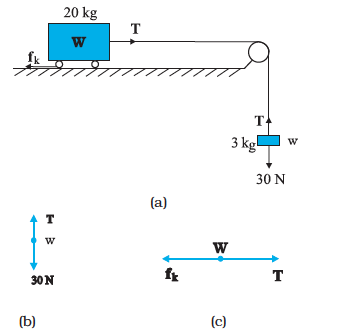
Answer As the string is inextensible, and the pully is smooth, the 3 kg block and the 20 kg trolley both have same magnitude of acceleration. Applying second law to motion of the block (Fig. 5.12(b)),

30 – T = 3a

Apply the second law to motion of the trolley (Fig. 5.12(c)),

T – fk = 20 a.

Now fk = µk N,

Here µk = 0.04,

N = 20 x 10

= 200 N.

Thus the equation for the motion of the trolley is

T – 0.04 x 200 = 20 a Or T – 8 = 20a.

These equations give a = 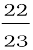m s –2 = 0.96 m s-2 and T = 27.1 N. 

Rolling friction

A body like a ring or a sphere rolling without slipping over a horizontal plane will suffer no friction, in principle. At every instant, there is just one point of contact between the body and the plane and this point has no motion relative to the plane. In this ideal situation, kinetic or static friction is zero and the body should continue to roll with constant velocity. We know, in practice, this will not happen and some resistance to motion (rolling friction) does occur, i.e. to keep the body rolling, some applied force is needed. For the same weight, rolling friction is much smaller (even by 2 or 3 orders of magnitude) than static or sliding friction. This is the reason why discovery of the wheel has been a major milestone in human history.

Rolling friction again has a complex origin, though somewhat different from that of static and sliding friction. During rolling, the surfaces in contact get momentarily deformed a little, and this results in a finite area (not a point) of the body being in contact with the surface. The net effect is that the component of the contact force parallel to the surface opposes motion.

We often regard friction as something undesirable. In many situations, like in a machine with different moving parts, friction does have a negative role. It opposes relative motion and thereby dissipates power in the form of heat, etc. Lubricants are a way of reducing kinetic friction in a machine. Another way is to use ball bearings between two moving parts of a machine [Fig. 5.13(a)]. Since the rolling friction between ball bearings and the surfaces in contact is very small, power dissipation is reduced. A thin cushion of air maintained between solid surfaces in relative motion is another effective way of reducing friction (Fig. 5.13(a)).

In many practical situations, however, friction is critically needed. Kinetic friction that dissipates power is nevertheless important for quickly stopping relative motion. It is made use of by brakes in machines and automobiles. Similarly, static friction is important in daily life. We are able to walk because of friction. It is impossible for a car to move on a very slippery road. On an ordinary road, the friction between the tyres and the road provides the necessary external force to accelerate the car.

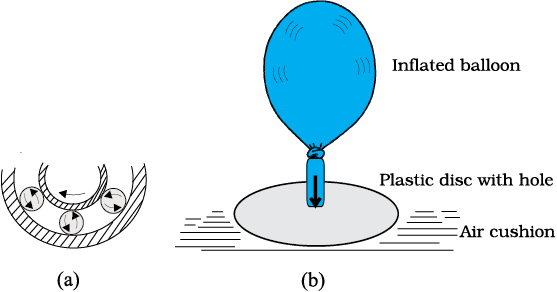
Fig. 5.13 Some ways of reducing friction. (a) Ball bearings placed between moving parts of a machine. (b) Compressed cushion of air between surfaces in relative motion.