As mentioned in section 4.2, vectors, by definition, obey the triangle law or equivalently, the parallelogram law of addition. We shall now describe this law of addition using the graphical method. Let us consider two vectors A and B that lie in a plane as shown in Fig. 4.4(a). The lengths of the line segments representing these vectors are proportional to the magnitude of the vectors. To find the sum A + B, we place vector B so that its tail is at the head of the vector A, as in Fig. 4.4(b). Then, we join the tail of A to the head of B. This line OQ represents a vector R, that is, the sum of the vectors A and B. Since, in this procedure of vector addition, vectors are arranged head to tail, this graphical method is called the head-to-tail method. The two vectors and their resultant form three sides of a triangle, so this method is also known as triangle method of vector addition. If we find the resultant of B + A as in Fig. 4.4(c), the same vector R is obtained. Thus, vector addition is commutative:
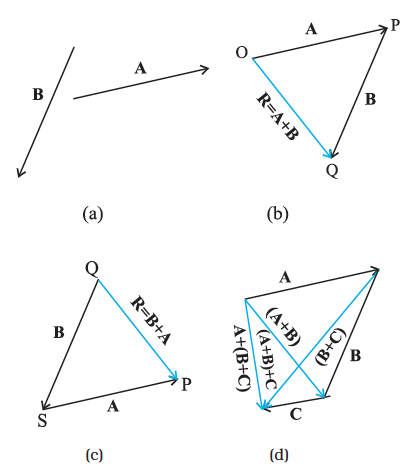
Fig. 4.4 (a) Vectors A and B. (b) Vectors A and B added graphically. (c) Vectors B and A added graphically. (d) Illustrating the associative law of vector addition.
A + B = B + A (4.1)
The addition of vectors also obeys the associative law as illustrated in Fig. 4.4(d). The result of adding vectors A and B first and then adding vector C is the same as the result of adding B and C first and then adding vector A :
(A + B) + C = A + (B + C) (4.2)
What is the result of adding two equal and opposite vectors ? Consider two vectors A and –A shown in Fig. 4.3(b). Their sum is A + (–A). Since the magnitudes of the two vectors are the same, but the directions are opposite, the resultant vector has zero magnitude and is represented by 0 called a null vector or a zero vector :
A – A = 0 |0|= 0 (4.3)
Since the magnitude of a null vector is zero, its direction cannot be specified.
The null vector also results when we multiply a vector A by the number zero. The main properties of 0 are :
A + 0 = A
λ 0 = 0
0 A = 0 (4.4)
What is the physical meaning of a zero vector? Consider the position and displacement vectors in a plane as shown in Fig. 4.1(a). Now suppose that an object which is at P at time t, moves to P′ and then comes back to P. Then, what is its displacement? Since the initial and final positions coincide, the displacement is a “null vector”.
Subtraction of vectors can be defined in terms of addition of vectors. We define the difference of two vectors A and B as the sum of two vectors A and –B :
A – B = A + (–B) (4.5)
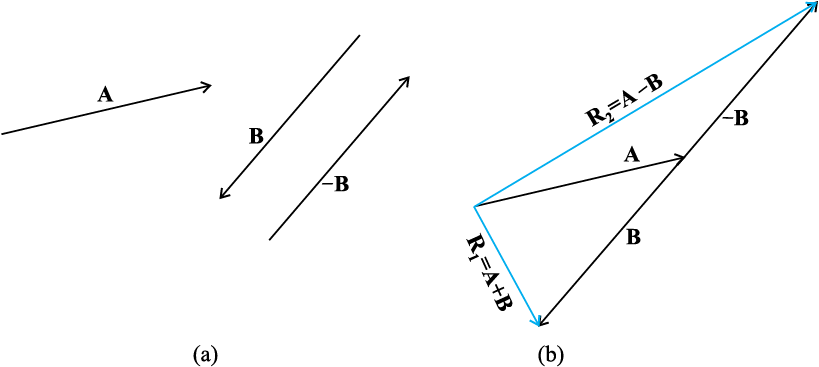
Fig. 4.5 (a) Two vectors A and B, – B is also shown. (b) Subtracting vector B from vector A – the result is R2. For comparison, addition of vectors A and B, i.e. R1 is also shown.
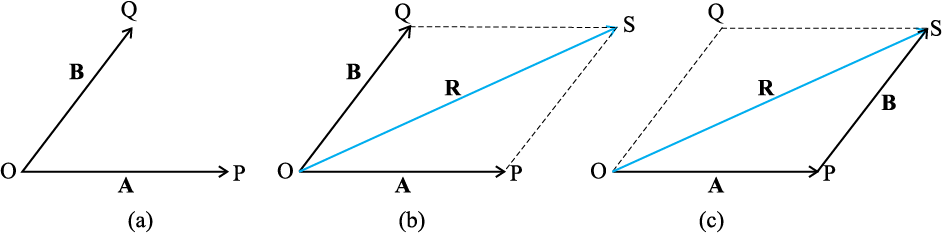
Fig. 4.6 (a) Two vectors A and B with their tails brought to a common origin. (b) The sum A+ B obtained using the parallelogram method. (c) The parallelogram method of vector addition is equivalent to the triangle method.
Example 4.1 Rain is falling vertically with a speed of 35 m s–1. Winds starts blowing after sometime with a speed of 12 m s–1 in east to west direction. In which direction should a boy waiting at a bus stop hold his umbrella ?
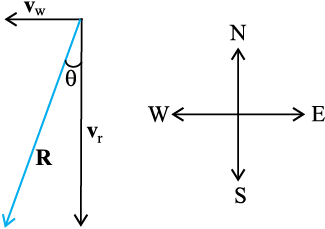
Fig. 4.7
Answer The velocity of the rain and the wind are represented by the vectors vr and vw in Fig. 4.7 and are in the direction specified by the problem. Using the rule of vector addition, we see that the resultant of vr and vw is R as shown in the figure. The magnitude of R is
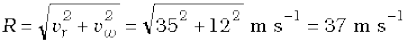
The direction θ that R makes with the vertical is given by
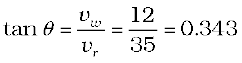
Or, 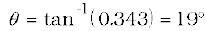
Therefore, the boy should hold his umbrella in the vertical plane at an angle of about 19o with the vertical towards the east.