8.1 Introduction
8.1 Introduction
8.2 Kepler’s laws
8.3 Universal law of gravitation
8.4 The gravitational constant
8.5 Acceleration due to gravity of the earth
8.6 Acceleration due to gravity below and above the surface of earth
8.7 Gravitational potential energy
8.8 Escape speed
8.9 Earth satellites
8.10 Energy of an orbiting satellite
8.11 Geostationary and polar satellites
8.12 Weightlessness
Summary
Points to ponder
Exercises
Additional exercises
Early in our lives, we become aware of the tendency of all material objects to be attracted towards the earth. Anything thrown up falls down towards the earth, going uphill is lot more tiring than going downhill, raindrops from the clouds above fall towards the earth and there are many other such phenomena. Historically it was the Italian Physicist Galileo (1564-1642) who recognised the fact that all bodies, irrespective of their masses, are accelerated towards the earth with a constant acceleration. It is said that he made a public demonstration of this fact. To find the truth, he certainly did experiments with bodies rolling down inclined planes and arrived at a value of the acceleration due to gravity which is close to the more accurate value obtained later.
A seemingly unrelated phenomenon, observation of stars, planets and their motion has been the subject of attention in many countries since the earliest of times. Observations since early times recognised stars which appeared in the sky with positions unchanged year after year. The more interesting objects are the planets which seem to have regular motions against the background of stars. The earliest recorded model for planetary motions proposed by Ptolemy about 2000 years ago was a ‘geocentric’ model in which all celestial objects, stars, the sun and the planets, all revolved around the earth. The only motion that was thought to be possible for celestial objects was motion in a circle. Complicated schemes of motion were put forward by Ptolemy in order to describe the observed motion of the planets. The planets were described as moving in circles with the centre of the circles themselves moving in larger circles. Similar theories were also advanced by Indian astronomers some 400 years later. However a more elegant model in which the Sun was the centre around which the planets revolved – the ‘heliocentric’ model – was already mentioned by Aryabhatta (5th century A.D.) in his treatise. A thousand years later, a Polish monk named Nicolas Copernicus (1473-1543) proposed a definitive model in which the planets moved in circles around a fixed central sun. His theory was discredited by the church, but notable amongst its supporters was Galileo who had to face prosecution from the state for his beliefs.
It was around the same time as Galileo, a nobleman called Tycho Brahe (1546-1601) hailing from Denmark, spent his entire lifetime recording observations of the planets with the naked eye. His compiled data were analysed later by his assistant Johannes Kepler (1571-1640). He could extract from the data three elegant laws that now go by the name of Kepler’s laws. These laws were known to Newton and enabled him to make a great scientific leap in proposing his universal law of gravitation.
The three laws of Kepler can be stated as follows:
1. Law of orbits : All planets move in elliptical orbits with the Sun situated at one of the foci of the ellipse (Fig. 8.1a). This law was a deviation from the Copernican model which allowed only circular orbits. The ellipse, of which the circle is a special case, is a closed curve which can be drawn very simply as follows.
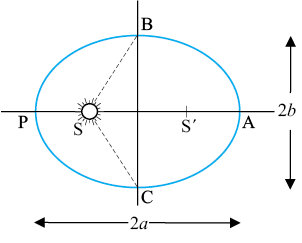
Fig. 8.1(a) An ellipse traced out by a planet around the sun. The closest point is P and the farthest point is A, P is called the perihelion and A the aphelion. The semimajor axis is half the distance AP.
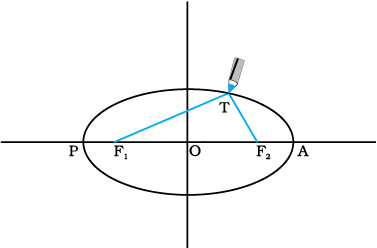
Fig. 8.1(b) Drawing an ellipse. A string has its ends fixed at F1 and F2. The tip of a pencil holds the string taut and is moved around.
* Refer to information given in the Box on Page 182
Select two points F1 and F2. Take a length of a string and fix its ends at F1 and F2 by pins. With the tip of a pencil stretch the string taut and then draw a curve by moving the pencil keeping the string taut throughout.(Fig. 8.1(b)) The closed curve you get is called an ellipse. Clearly for any point T on the ellipse, the sum of the distances from F1 and F2 is a constant. F1, F2 are called the focii. Join the points F1 and F2 and extend the line to intersect the ellipse at points P and A as shown in Fig. 8.1(b). The midpoint of the line PA is the centre of the ellipse O and the length PO = AO is called the semi-major axis of the ellipse. For a circle, the two focii merge into one and the semi-major axis becomes the radius of the circle.
2. Law of areas : The line that joins any planet to the sun sweeps equal areas in equal intervals of time (Fig. 8.2). This law comes from the observations that planets appear to move slower when they are farther from the sun than when they are nearer.
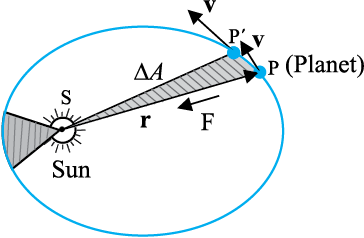
Fig. 8.2 The planet P moves around the sun in an elliptical orbit. The shaded area is the area ∆A swept out in a small interval of time ∆t.
3. Law of periods : The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.
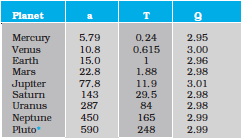
Table 8.1 gives the approximate time periods of revolution of eight* planets around the sun along with values of their semi-major axes.
(a ≡ Semi-major axis in units of 1010 m.
T ≡ Time period of revolution of the planet in years(y).
Q ≡ The quotient ( T2/a3 ) in units of 10 -34 y2 m-3.)
The law of areas can be understood as a consequence of conservation of angular momentum whch is valid for any central force . A central force is such that the force on the planet is along the vector joining the Sun and the planet. Let the Sun be at the origin and let the position and momentum of the planet be denoted by r and p respectively. Then the area swept out by the planet of mass m in time interval ∆t is (Fig. 8.2) ∆A given by
∆A = ½ (r × v∆t) (8.1)
Hence
∆A /∆t =½ (r × p)/m, (since v = p/m)
= L / (2 m) (8.2)
where v is the velocity, L is the angular momentum equal to ( r × p). For a central force, which is directed along r, L is a constant as the planet goes around. Hence, ∆A /∆t is a constant according to the last equation. This is the law of areas. Gravitation is a central force and hence the law of areas follows.

Johannes Kepler (1571–1630) was a scientist of German origin. He formulated the three laws of planetary motion based on the painstaking observations of Tycho Brahe and coworkers. Kepler himself was an assistant to Brahe and it took him sixteen long years to arrive at the three planetary laws. He is also known as the founder of geometrical optics, being the first to describe what happens to light after it enters a telescope.
* Refer to information given in the Box on Page 182
Example 8.1 Let the speed of the planet at the perihelion P in Fig. 8.1(a) be vP and the Sun-planet distance SP be rP. Relate {rP, vP} to the corresponding quantities at the aphelion {rA, vA}. Will the planet take equal times to traverse BAC and CPB ?
Answer The magnitude of the angular momentum at P is Lp = mp rp vp, since inspection tells us that rp and vp are mutually perpendicular. Similarly, LA = mp rA vA. From angular momentum conservation
mp rp vp = mp rA vA
or 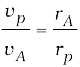
Since rA > rp, vp > vA .
The area SBAC bounded by the ellipse and the radius vectors SB and SC is larger than SBPC in Fig. 8.1. From Kepler’s second law, equal areas are swept in equal times. Hence the planet will take a longer time to traverse BAC than CPB.
Legend has it that observing an apple falling from a tree, Newton was inspired to arrive at an universal law of gravitation that led to an explanation of terrestrial gravitation as well as of Kepler’s laws. Newton’s reasoning was that the moon revolving in an orbit of radius Rm was subject to a centripetal acceleration due to earth’s gravity of magnitude
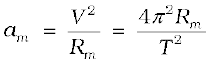
where V is the speed of the moon related to the time period T by the relation 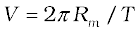 . The time period T is about 27.3 days and Rm was already known then to be about 3.84 × 108m. If we substitute these numbers in Eq. (8.3), we get a value of am much smaller than the value of acceleration due to gravity g on the surface of the earth, arising also due to earth’s gravitational attraction.
. The time period T is about 27.3 days and Rm was already known then to be about 3.84 × 108m. If we substitute these numbers in Eq. (8.3), we get a value of am much smaller than the value of acceleration due to gravity g on the surface of the earth, arising also due to earth’s gravitational attraction.
We know the time rate of change of the angular momentum of a single particle about the origin is
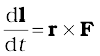
The angular momentum of the particle is conserved, if the torque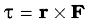 due to the force F on it vanishes. This happens either when F is zero or when F is along r. We are interested in forces which satisfy the latter condition. Central forces satisfy this condition.
due to the force F on it vanishes. This happens either when F is zero or when F is along r. We are interested in forces which satisfy the latter condition. Central forces satisfy this condition.
A ‘central’ force is always directed towards or away from a fixed point, i.e., along the position vector of the point of application of the force with respect to the fixed point. (See Figure below.) Further, the magnitude of a central force F depends on r, the distance of the point of application of the force from the fixed point; F = F(r).
In the motion under a central force the angular momentum is always conserved. Two important results follow from this:
(1) The motion of a particle under the central force is always confined to a plane.
(2) The position vector of the particle with respect to the centre of the force (i.e. the fixed point) has a constant areal velocity. In other words the position vector sweeps out equal areas in equal times as the particle moves under the influence of the central force.
Try to prove both these results. You may need to know that the areal velocity is given by :
dA/dt = ½ r v sin α.
An immediate application of the above discussion can be made to the motion of a planet under the gravitational force of the sun. For convenience the sun may be taken to be so heavy that it is at rest. The gravitational force of the sun on the planet is directed towards the sun. This force also satisfies the requirement F = F(r), since F = G m1m2/r2 where m1and m2 are respectively the masses of the planet and the sun and G is the universal constant of gravitation. The two results (1) and (2) described above, therefore, apply to the motion of the planet. In fact, the result (2) is the well-known second law of Kepler.
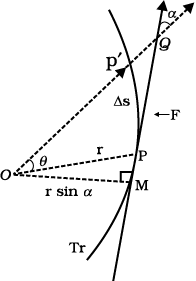
Tr is the trejectory of the particle under the central force. At a position P, the force is directed along OP, O is the centre of the force taken as the origin. In time ∆t, the particle moves from P to P′, arc PP′ = ∆s = v ∆t. The tangent PQ at P to the trajectory gives the direction of the velocity at P. The area swept in ∆t is the area of sector POP′ ≈ (r sin α ) PP′/2 = (r v sin a) ∆t/2.)
This clearly shows that the force due to earth’s gravity decreases with distance. If one assumes that the gravitational force due to the earth decreases in proportion to the inverse square of the distance from the centre of the earth, we will have
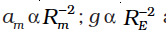
and we get
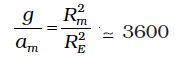
(8.4)
in agreement with a value of g ≅ 9.8 m s-2 and the value of am from Eq. (8.3). These observations led Newton to propose the following Universal Law of Gravitation :
Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
The quotation is essentially from Newton’s famous treatise called ‘Mathematical Principles of Natural Philosophy’ (Principia for short).
Stated Mathematically, Newton’s gravitation law reads : The force F on a point mass m2 due to another point mass m1 has the magnitude
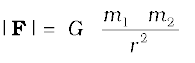
Equation (8.5) can be expressed in vector form as
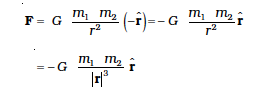
where G is the universal gravitational constant, 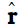 is the unit vector from m1 to m2 and r = r2 – r1 as shown in Fig. 8.3.
is the unit vector from m1 to m2 and r = r2 – r1 as shown in Fig. 8.3.
The gravitational force is attractive, i.e., the force F is along – r. The force on point mass m1 due to m2 is of course – F by Newton’s third law. Thus, the gravitational force F12 on the body 1 due to 2 and F21 on the body 2 due to 1 are related as F12 = – F21.
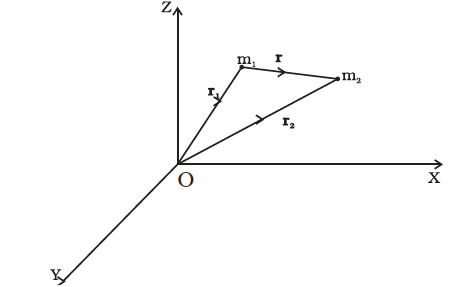
Fig. 8.3 Gravitational force on m1 due to m2 is along r where the vector r is (r2– r1).
Before we can apply Eq. (8.5) to objects under consideration, we have to be careful since the law refers to point masses whereas we deal with extended objects which have finite size. If we have a collection of point masses, the force on any one of them is the vector sum of the gravitational forces exerted by the other point masses as shown in Fig 8.4.
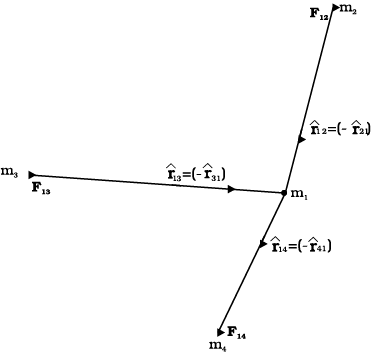
Fig. 8.4 Gravitational force on point mass m1 is the vector sum of the gravitational forces exerted by m2, m3 and m4.
The total force on m1 is
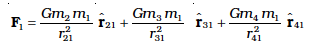
Example 8.2 Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC.
(a) What is the force acting on a mass 2m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled ?
Take AG = BG = CG = 1 m (see Fig. 8.5)
Answer (a) The angle between GC and the positive x-axis is 30° and so is the angle between GB and the negative x-axis. The individual forces in vector notation are
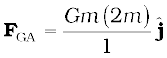
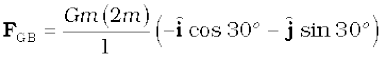
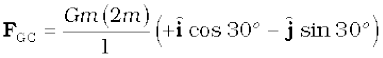
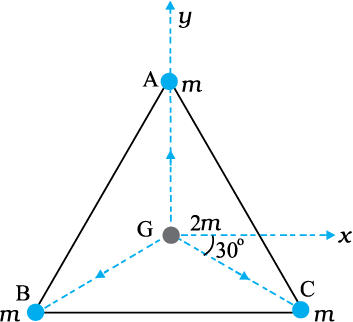
Fig. 8.5 Three equal masses are placed at the three vertices of the ∆ ABC. A mass 2m is placed at the centroid G.
From the principle of superposition and the law of vector addition, the resultant gravitational force FR on (2m) is
FR = FGA + FGB + FGC
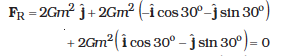
Alternatively, one expects on the basis of symmetry that the resultant force ought to be zero.
(b) Now if the mass at vertex A is doubled then
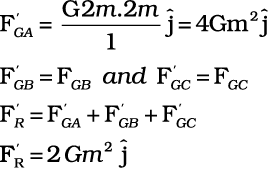
For the gravitational force between an extended object (like the earth) and a point mass, Eq. (8.5) is not directly applicable. Each point mass in the extended object will exert a force on the given point mass and these force will not all be in the same direction. We have to add up these forces vectorially for all the point masses in the extended object to get the total force. This is easily done using calculus. For two special cases, a simple law results when you do that :
(1) The force of attraction between a hollow spherical shell of uniform density and a point mass situated outside is just as if the entire mass of the shell is concentrated at the centre of the shell.
Qualitatively this can be understood as follows: Gravitational forces caused by the various regions of the shell have components along the line joining the point mass to the centre as well as along a direction prependicular to this line. The components prependicular to this line cancel out when summing over all regions of the shell leaving only a resultant force along the line joining the point to the centre. The magnitude of this force works out to be as stated above.
Kepler had formulated his third law by 1619. The announcement of the underlying universal law of gravitation came about seventy years later with the publication in 1687 of Newton’s masterpiece Philosophiae Naturalis Principia Mathematica, often simply called thePrincipia.
Around 1685, Edmund Halley (after whom the famous Halley’s comet is named), came to visit Newton at Cambridge and asked him about the nature of the trajectory of a body moving under the influence of an inverse square law. Without hesitation Newton replied that it had to be an ellipse, and further that he had worked it out long ago around 1665 when he was forced to retire to his farm house from Cambridge on account of a plague outbreak. Unfortunately, Newton had lost his papers. Halley prevailed upon Newton to produce his work in book form and agreed to bear the cost of publication. Newton accomplished this feat in eighteen months of superhuman effort. The Principia is a singular scientific masterpiece and in the words of Lagrange it is “the greatest production of the human mind.” The Indian born astrophysicist and Nobel laureate S. Chandrasekhar spent ten years writing a treatise on the Principia. His book, Newton’s Principia for the Common Reader brings into sharp focus the beauty, clarity and breath taking economy of Newton’s methods.
(2) The force of attraction due to a hollow spherical shell of uniform density, on a point mass situated inside it is zero.
Qualitatively, we can again understand this result. Various regions of the spherical shell attract the point mass inside it in various directions. These forces cancel each other completely.
The value of the gravitational constant G entering the Universal law of gravitation can be determined experimentally and this was first done by English scientist Henry Cavendish in 1798. The apparatus used by him is schematically shown in figure.8.6
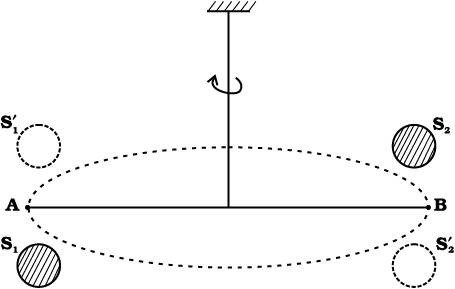
Fig. 8.6 Schematic drawing of Cavendish’s experiment. S1 and S2 are large spheres which are kept on either side (shown shades) of the masses at A and B. When the big spheres are taken to the other side of the masses (shown by dotted circles), the bar AB rotates a little since the torque reverses direction. The angle of rotation can be measured experimentally.
The bar AB has two small lead spheres attached at its ends. The bar is suspended from a rigid support by a fine wire. Two large lead spheres are brought close to the small ones but on opposite sides as shown. The big spheres attract the nearby small ones by equal and opposite force as shown. There is no net force on the bar but only a torque which is clearly equal to F times the length of the bar,where F is the force of attraction between a big sphere and its neighbouring small sphere. Due to this torque, the suspended wire gets twisted till such time as the restoring torque of the wire equals the gravitational torque . If θ is the angle of twist of the suspended wire, the restoring torque is proportional to θ, equal to τθ. Where τ is the restoring couple per unit angle of twist. τ can be measured independently e.g. by applying a known torque and measuring the angle of twist. The gravitational force between the spherical balls is the same as if their masses are concentrated at their centres. Thus if d is the separation between the centres of the big and its neighbouring small ball, M and m their masses, the gravitational force between the big sphere and its neighouring small ball is.
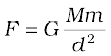
If L is the length of the bar AB , then the torque arising out of F is F multiplied by L. At equilibrium, this is equal to the restoring torque and hence
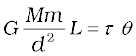
Observation of θ thus enables one to calculate G from this equation.
Since Cavendish’s experiment, the measurement of G has been refined and the currently accepted value is
G = 6.67×10-11 N m2/kg2 (8.8)
The earth can be imagined to be a sphere made of a large number of concentric spherical shells with the smallest one at the centre and the largest one at its surface. A point outside the earth is obviously outside all the shells. Thus, all the shells exert a gravitational force at the point outside just as if their masses are concentrated at their common centre according to the result stated in section 8.3. The total mass of all the shells combined is just the mass of the earth. Hence, at a point outside the earth, the gravitational force is just as if its entire mass of the earth is concentrated at its centre.
For a point inside the earth, the situation is different. This is illustrated in Fig. 8.7.
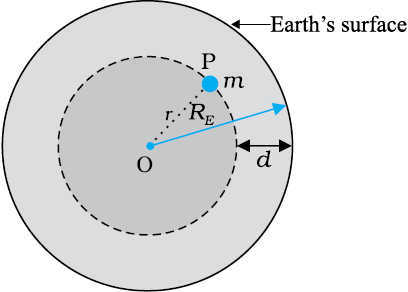
Fig. 8.7 The mass m is in a mine located at a depth d below the surface of the Earth of mass ME and radius RE. We treat the Earth to be spherically symmetric.
Again consider the earth to be made up of concentric shells as before and a point mass m situated at a distance r from the centre. The point P lies outside the sphere of radius r. For the shells of radius greater than r, the point P lies inside. Hence according to result stated in the last section, they exert no gravitational force on mass m kept at P. The shells with radius ≤ r make up a sphere of radius r for which the point P lies on the surface. This smaller sphere therefore exerts a force on a mass m at P as if its mass Mr is concentrated at the centre. Thus the force on the mass m at P has a magnitude
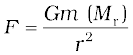
We assume that the entire earth is of uniform density and hence its mass is 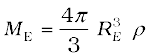 where ME is the mass of the earth RE is its radius and ρ is the density. On the other hand the mass of the sphere Mr of radius r is
where ME is the mass of the earth RE is its radius and ρ is the density. On the other hand the mass of the sphere Mr of radius r is 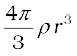 and hence
and hence
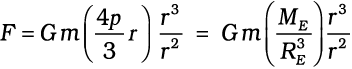
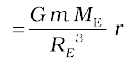
If the mass m is situated on the surface of earth, then r = RE and the gravitational force on it is, from Eq. (8.10)
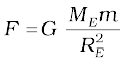
The acceleration experienced by the mass m, which is usually denoted by the symbol g is related to F by Newton’s 2nd law by relation F = mg. Thus
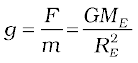
Acceleration g is readily measurable. RE is a known quantity. The measurement of G by Cavendish’s experiment (or otherwise), combined with knowledge of g and RE enables one to estimate ME from Eq. (8.12). This is the reason why there is a popular statement regarding Cavendish : “Cavendish weighed the earth”.
Consider a point mass m at a height h above the surface of the earth as shown in Fig. 8.8(a). The radius of the earth is denoted by RE . Since this point is outside the earth, its distance from the centre of the earth is (RE + h ). If F (h) denoted the magnitude of the force on the point mass m , we get from Eq. (8.5) :
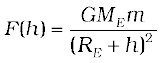
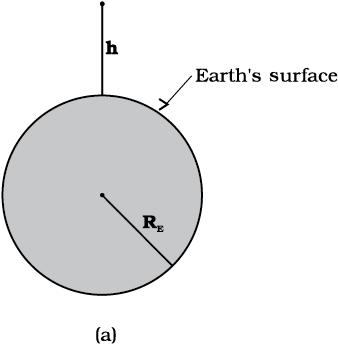
Fig. 8.8 (a) g at a height h above the surface of the earth.
The acceleration experienced by the point mass is 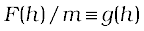 and we get
and we get
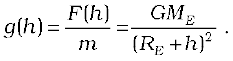
This is clearly less than the value of g on the surface of earth : 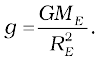 For
For 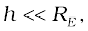 we can expand the RHS of Eq. (8.14) :
we can expand the RHS of Eq. (8.14) :
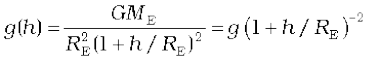
For 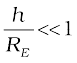 , using binomial expression,
, using binomial expression,
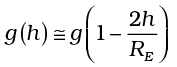
Equation (8.15) thus tells us that for small heights h above the value of g decreases by a factor 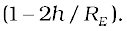
Now, consider a point mass m at a depth d below the surface of the earth (Fig. 8.8(b)), so that its distance from the centre of the earth is 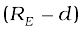 as shown in the figure. The earth can be thought of as being composed of a smaller sphere of radius (RE – d ) and a spherical shell of thickness d. The force on m due to the outer shell of thickness d is zero because the result quoted in the previous section. As far as the smaller sphere of radius ( RE – d ) is concerned, the point mass is outside it and hence according to the result quoted earlier, the force due to this smaller sphere is just as if the entire mass of the smaller sphere is concentrated at the centre. If Ms is the mass of the smaller sphere, then,
as shown in the figure. The earth can be thought of as being composed of a smaller sphere of radius (RE – d ) and a spherical shell of thickness d. The force on m due to the outer shell of thickness d is zero because the result quoted in the previous section. As far as the smaller sphere of radius ( RE – d ) is concerned, the point mass is outside it and hence according to the result quoted earlier, the force due to this smaller sphere is just as if the entire mass of the smaller sphere is concentrated at the centre. If Ms is the mass of the smaller sphere, then,
Ms/ME = ( RE – d)3 / RE3 ( 8.16)
Since mass of a sphere is proportional to be cube of its radius.
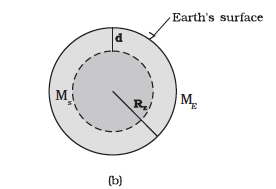
Fig. 8.8 (b) g at a depth d. In this case only the smaller sphere of radius (RE–d) contributes to g.
Thus the force on the point mass is
F (d) = G Ms m / (RE – d ) 2 (8.17)
Substituting for Ms from above , we get
F (d) = G ME m ( RE – d ) / RE 3 (8.18)
and hence the acceleration due to gravity at a depth d,
g(d) = 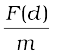 is
is
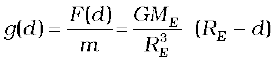
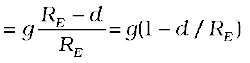
Thus, as we go down below earth’s surface, the acceleration due gravity decreases by a factor 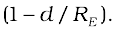 The remarkable thing about acceleration due to earth’s gravity is that it is maximum on its surface decreasing whether you go up or down.
The remarkable thing about acceleration due to earth’s gravity is that it is maximum on its surface decreasing whether you go up or down.
We had discussed earlier the notion of potential energy as being the energy stored in the body at its given position. If the position of the particle changes on account of forces acting on it, then the change in its potential energy is just the amount of work done on the body by the force. As we had discussed earlier, forces for which the work done is independent of the path are the conservative forces.
The force of gravity is a conservative force and we can calculate the potential energy of a body arising out of this force, called the gravitational potential energy. Consider points close to the surface of earth, at distances from the surface much smaller than the radius of the earth. In such cases, the force of gravity is practically a constant equal to mg, directed towards the centre of the earth. If we consider a point at a height h1 from the surface of the earth and another point vertically above it at a height h2 from the surface, the work done in lifting the particle of mass m from the first to the second position is denoted by W12
W12 = Force × displacement
= mg (h2 – h1) (8.20)
If we associate a potential energy W(h) at a point at a height h above the surface such that
W(h) = mgh + Wo (8.21)
(where Wo = constant) ;
then it is clear that
W12 = W(h2) – W(h1) (8.22)
The work done in moving the particle is just the difference of potential energy between its final and initial positions.Observe that the constant Wo cancels out in Eq. (8.22). Setting h = 0 in the last equation, we get W ( h = 0 ) = Wo. . h = 0 means points on the surface of the earth. Thus, Wo is the potential energy on the surface of the earth.
If we consider points at arbitrary distance from the surface of the earth, the result just derived is not valid since the assumption that the gravitational force mg is a constant is no longer valid. However, from our discussion we know that a point outside the earth, the force of gravitation on a particle directed towards the centre of the earth is
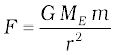
where ME = mass of earth, m = mass of the particle and r its distance from the centre of the earth. If we now calculate the work done in lifting a particle from r = r1 to r = r2 (r2 > r1) along a vertical path, we get instead of Eq. (8.20)
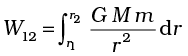
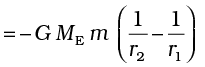
In place of Eq. (8.21), we can thus associate a potential energy W(r) at a distance r, such that
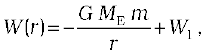
valid for r > R ,
so that once again W12 = W(r2) – W(r1). Setting r = infinity in the last equation, we get W ( r = infinity ) = W1 . Thus, W1 is the potential energy at infinity. One should note that only the difference of potential energy between two points has a definite meaning from Eqs. (8.22) and (8.24). One conventionally sets W1 equal to zero, so that the potential energy at a point is just the amount of work done in displacing the particle from infinity to that point.
We have calculated the potential energy at a point of a particle due to gravitational forces on it due to the earth and it is proportional to the mass of the particle. The gravitational potential due to the gravitational force of the earth is defined as the potential energy of a particle of unit mass at that point. From the earlier discussion, we learn that the gravitational potential energy associated with two particles of masses m1 and m2 separated by distance by a distance r is given by
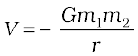 (if we choose V = 0 as r → ∞ )
(if we choose V = 0 as r → ∞ )
It should be noted that an isolated system of particles will have the total potential energy that equals the sum of energies (given by the above equation) for all possible pairs of its constituent particles. This is an example of the application of the superposition principle.
Example 8.3 Find the potential energy of a system of four particles placed at the vertices of a square of side l. Also obtain the potential at the centre of the square.
Answer Consider four masses each of mass m at the corners of a square of side l; See Fig. 8.9. We have four mass pairs at distance l and two diagonal pairs at distance 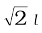
Hence,
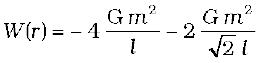
Fig. 8.9
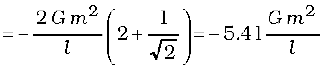
The gravitational potential at the centre of the square 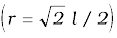 is
is
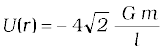
If a stone is thrown by hand, we see it falls back to the earth. Of course using machines we can shoot an object with much greater speeds and with greater and greater initial speed, the object scales higher and higher heights. A natural query that arises in our mind is the following: ‘can we throw an object with such high initial speeds that it does not fall back to the earth?’
The principle of conservation of energy helps us to answer this question. Suppose the object did reach infinity and that its speed there was Vf. The energy of an object is the sum of potential and kinetic energy. As before W1 denotes that gravitational potential energy of the object at infinity. The total energy of the projectile at infinity then is
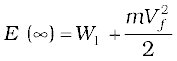
If the object was thrown initially with a speed Vi from a point at a distance (h+RE) from the centre of the earth (RE = radius of the earth), its energy initially was
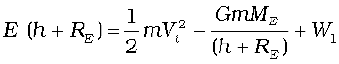
By the principle of energy conservation Eqs. (8.26) and (8.27) must be equal. Hence
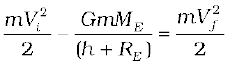
The R.H.S. is a positive quantity with a minimum value zero hence so must be the L.H.S. Thus, an object can reach infinity as long as Vi is such that
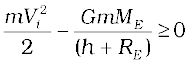
The minimum value of Vi corresponds to the case when the L.H.S. of Eq. (8.29) equals zero. Thus, the minimum speed required for an object to reach infinity (i.e. escape from the earth) corresponds to
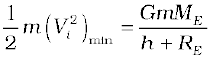
If the object is thrown from the surface of the earth, h = 0, and we get
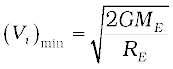
Using the relation 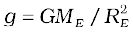 , we get
, we get
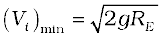
Using the value of g and RE, numerically (Vi)min≈11.2 km/s. This is called the escape speed, sometimes loosely called the escape velocity.
Equation (8.32) applies equally well to an object thrown from the surface of the moon with g replaced by the acceleration due to Moon’s gravity on its surface and rE replaced by the radius of the moon. Both are smaller than their values on earth and the escape speed for the moon turns out to be 2.3 km/s, about five times smaller. This is the reason that moon has no atmosphere. Gas molecules if formed on the surface of the moon having velocities larger than this will escape the gravitational pull of the moon.
Example 8.4 Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in Fig. 8.10. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
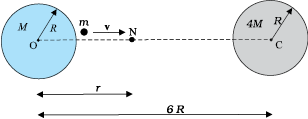
Fig. 8.10
Answer The projectile is acted upon by two mutually opposing gravitational forces of the two spheres. The neutral point N (see Fig. 8.10) is defined as the position where the two forces cancel each other exactly. If ON = r, we have
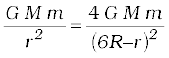
(6R – r)2 = 4r2
6R – r = ±2r
r = 2R or – 6R.
The neutral point r = – 6R does not concern us in this example. Thus ON = r = 2R. It is sufficient to project the particle with a speed which would enable it to reach N. Thereafter, the greater gravitational pull of 4M would suffice. The mechanical energy at the surface of M is
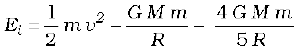 .
.
At the neutral point N, the speed approaches zero. The mechanical energy at N is purely potential.
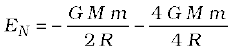 .
.
From the principle of conservation of mechanical energy
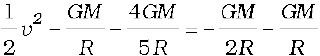
or 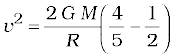
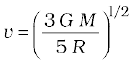
A point to note is that the speed of the projectile is zero at N, but is nonzero when it strikes the heavier sphere 4 M. The calculation of this speed is left as an exercise to the students.
Earth satellites are objects which revolve around the earth. Their motion is very similar to the motion of planets around the Sun and hence Kepler’s laws of planetary motion are equally applicable to them. In particular, their orbits around the earth are circular or elliptic. Moon is the only natural satellite of the earth with a near circular orbit with a time period of approximately 27.3 days which is also roughly equal to the rotational period of the moon about its own axis. Since, 1957, advances in technology have enabled many countries including India to launch artificial earth satellites for practical use in fields like telecommunication, geophysics and meteorology.
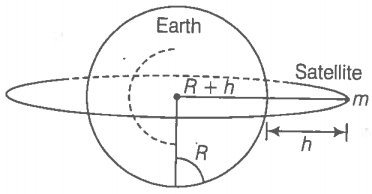
We will consider a satellite in a circular orbit of a distance (RE + h) from the centre of the earth, where RE = radius of the earth. If m is the mass of the satellite and V its speed, the centripetal force required for this orbit is
F(centripetal) = 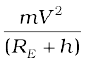
directed towards the centre. This centripetal force is provided by the gravitational force, which is
F(gravitation) = 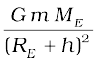
where ME is the mass of the earth.
Equating R.H.S of Eqs. (8.33) and (8.34) and cancelling out m, we get
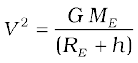
Thus V decreases as h increases. From equation (8.35),the speed V for h = 0 is
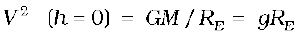
where we have used the relation
g =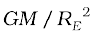 . In every orbit, the satellite traverses a distance 2π(RE + h) with speed V. Its time period T therefore is
. In every orbit, the satellite traverses a distance 2π(RE + h) with speed V. Its time period T therefore is
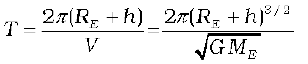
on substitution of value of V from Eq. (8.35). Squaring both sides of Eq. (8.37), we get
T 2 = k ( RE + h)3 (where k = 4 π2 / GME) (8.38)
which is Kepler’s law of periods, as applied to motion of satellites around the earth. For a satellite very close to the surface of earth h can be neglected in comparison to RE in Eq. (8.38). Hence, for such satellites, T is To, where
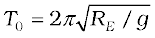
If we substitute the numerical values g ≅ 9.8 m s-2 and RE = 6400 km., we get
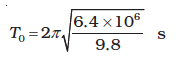
Which is approximately 85 minutes.
Example 8.5 The planet Mars has two moons, phobos and delmos. (i) phobos has a period 7 hours, 39 minutes and an orbital radius of 9.4 ×103 km. Calculate the mass of mars. (ii) Assume that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. What is the length of the martian year in days ?
Answer (i) We employ Eq. (8.38) with the sun’s mass replaced by the martian mass Mm
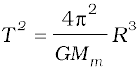
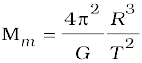
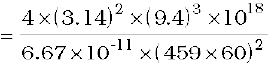
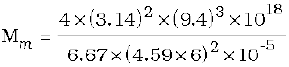
= 6.48 × 1023 kg.
(ii) Once again Kepler’s third law comes to our aid,
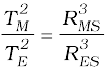
where RMS is the mars -sun distance and RES is the earth-sun distance.
∴ TM = (1.52)3/2 × 365
= 684 days
We note that the orbits of all planets except Mercury, Mars and Pluto* are very close to being circular. For example, the ratio of the semi-minor to semi-major axis for our Earth is, b/a = 0.99986.
Example 8.6 Weighing the Earth : You are given the following data: g = 9.81 ms–2, RE = 6.37×106 m, the distance to the moon R = 3.84×108 m and the time period of the moon’s revolution is 27.3 days. Obtain the mass of the Earth ME in two different ways.
Answer From Eq. (8.12) we have
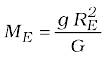
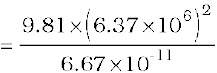
= 5.97× 1024 kg.
The moon is a satellite of the Earth. From the derivation of Kepler’s third law [see Eq. (8.38)]
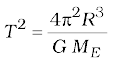
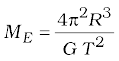
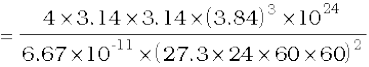
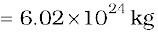
Both methods yield almost the same answer, the difference between them being less than 1%.
Example 8.7 Express the constant k of Eq. (8.38) in days and kilometres. Given k = 10–13 s2 m–3. The moon is at a distance of 3.84 × 105 km from the earth. Obtain its time-period of revolution in days.
Answer Given
k = 10–13 s2 m–3
= 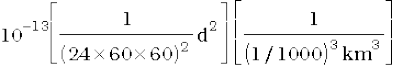
= 1.33 ×10–14 d2 km–3
Using Eq. (8.38) and the given value of k, the time period of the moon is
T2 = (1.33 × 10-14)(3.84 × 105)3
T = 27.3 d
Note that Eq. (8.38) also holds for elliptical orbits if we replace (RE+h) by the semi-major axis of the ellipse. The earth will then be at one of the foci of this ellipse.
Using Eq. (8.35), the kinetic energy of the satellite in a circular orbit with speed v is
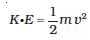
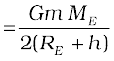
Considering gravitational potential energy at infinity to be zero, the potential energy at distance (RE+h) from the centre of the earth is
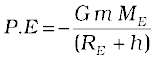
The K.E is positive whereas the P.E is negative. However, in magnitude the K.E. is half the P.E, so that the total E is
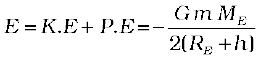
The total energy of an circularly orbiting satellite is thus negative, with the potential energy being negative but twice is magnitude of the positive kinetic energy.
When the orbit of a satellite becomes elliptic, both the K.E. and P.E. vary from point to point. The total energy which remains constant is negative as in the circular orbit case. This is what we expect, since as we have discussed before if the total energy is positive or zero, the object escapes to infinity. Satellites are always at finite distance from the earth and hence their energies cannot be positive or zero.
Example 8.8 A 400 kg satellite is in a circular orbit of radius 2RE about the Earth. How much energy is required to transfer it to a circular orbit of radius 4RE ? What are the changes in the kinetic and potential energies ?
Answer Initially,
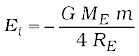
While finally
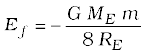
The change in the total energy is
∆E = Ef – Ei
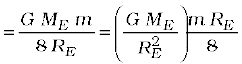
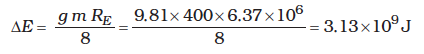
The kinetic energy is reduced and it mimics ∆E, namely, ∆K = Kf – Ki = – 3.13 × 109 J.
The change in potential energy is twice the change in the total energy, namely
∆V = Vf – Vi = – 6.25 × 109 J
An interesting phenomenon arises if in we arrange the value of (RE+ h) such that T in
Eq. (8.37) becomes equal to 24 hours. If the circular orbit is in the equatorial plane of the earth, such a satellite, having the same period as the period of rotation of the earth about its own axis would appear stationery viewed from a point on earth. The (RE + h) for this purpose works out to be large as compared to RE :
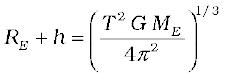
and for T = 24 hours, h works out to be 35800 km. which is much larger than RE. Satellites in a circular orbits around the earth in the equatorial plane with T = 24 hours are called Geostationery Satellites. Clearly, since the earth rotates with the same period, the satellite would appear fixed from any point on earth. It takes very powerful rockets to throw up a satellite to such large heights above the earth but this has been done in view of the several benefits of many practical applications.

Fig. 8.11 A Polar satellite. A strip on earth’s surface (shown shaded) is visible from the satellite during one cycle. For the next revolution of the satellite, the earth has rotated a little on its axis so that an adjacent strip becomes visible.
It is known that electromagnetic waves above a certain frequency are not reflected from ionosphere. Radio waves used for radio broadcast which are in the frequency range 2 MHz to 10 MHz, are below the critical frequency. They are therefore reflected by the ionosphere.
Weight of an object is the force with which the earth attracts it. We are conscious of our own weight when we stand on a surface, since the surface exerts a force opposite to our weight to keep us at rest. The same principle holds good when we measure the weight of an object by a spring balance hung from a fixed point e.g. the ceiling. The object would fall down unless it is subject to a force opposite to gravity. This is exactly what the spring exerts on the object. This is because the spring is pulled down a little by the gravitational pull of the object and in turn the spring exerts a force on the object vertically upwards.
Now, imagine that the top end of the balance is no longer held fixed to the top ceiling of the room. Both ends of the spring as well as the object move with identical acceleration g. The spring is not stretched and does not exert any upward force on the object which is moving down with acceleration g due to gravity. The reading recorded in the spring balance is zero since the spring is not stretched at all. If the object were a human being, he or she will not feel his weight since there is no upward force on him. Thus, when an object is in free fall, it is weightless and this phenomenon is usually called the phenomenon of weightlessness.
In a satellite around the earth, every part and parcel of the satellite has an acceleration towards the centre of the earth which is exactly the value of earth’s acceleration due to gravity at that position. Thus in the satellite everything inside it is in a state of free fall. This is just as if we were falling towards the earth from a height. Thus, in a manned satellite, people inside experience no gravity. Gravity for us defines the vertical direction and thus for them there are no horizontal or vertical directions, all directions are the same. Pictures of astronauts floating in a satellite show this fact.
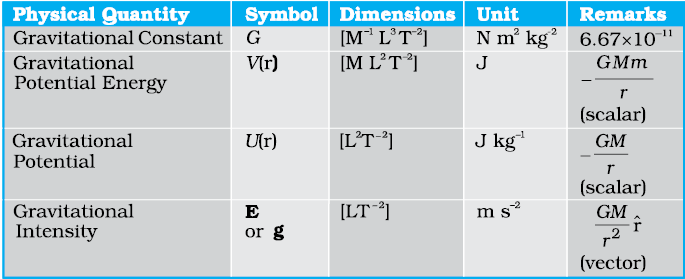
1. Newton’s law of universal gravitation states that the gravitational force of attraction between any two particles of masses m1 and m2 separated by a distance r has the magnitude
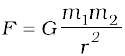
where G is the universal gravitational constant, which has the value 6.672 ×10–11 N m2 kg–2.
2. If we have to find the resultant gravitational force acting on the particle m due to a number of masses M1, M2, ….Mn etc. we use the principle of superposition. Let F1, F2, ….Fn be the individual forces due to M1, M2, ….Mn, each given by the law of gravitation. From the principle of superposition each force acts independently and uninfluenced by the other bodies. The resultant force FR is then found by vector addition
FR = F1 + F2 + ……+ Fn = 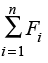
where the symbol ‘Σ’ stands for summation.
3. Kepler’s laws of planetary motion state that
(a) All planets move in elliptical orbits with the Sun at one of the focal points
(b) The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals. This follows from the fact that the force of gravitation on the planet is central and hence angular momentum is conserved.
(c) The square of the orbital period of a planet is proportional to the cube of the semi-major axis of the elliptical orbit of the planet
The period T and radius R of the circular orbit of a planet about the Sun are related by
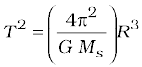
where Ms is the mass of the Sun. Most planets have nearly circular orbits about the Sun. For elliptical orbits, the above equation is valid if R is replaced by the semi-major axis, a.
4. The acceleration due to gravity.
(a) at a height h above the earth’s surface
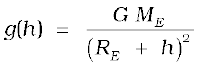
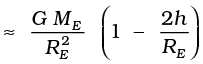 for h << RE
for h << RE
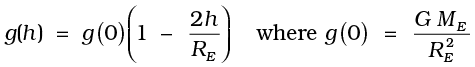
(b) at depth d below the earth’s surface is
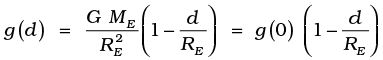
5. The gravitational force is a conservative force, and therefore a potential energy function can be defined. The gravitational potential energy associated with two particles separated by a distance r is given by
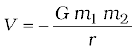
where V is taken to be zero at r → ∞. The total potential energy for a system of particles is the sum of energies for all pairs of particles, with each pair represented by a term of the form given by above equation. This prescription follows from the principle of superposition.
6. If an isolated system consists of a particle of mass m moving with a speed v in the vicinity of a massive body of mass M, the total mechanical energy of the particle is given by
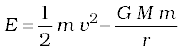
That is, the total mechanical energy is the sum of the kinetic and potential energies. The total energy is a constant of motion.
7. If m moves in a circular orbit of radius a about M, where M >> m, the total energy of the system is
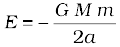
with the choice of the arbitrary constant in the potential energy given in the point 5., above. The total energy is negative for any bound system, that is, one in which the orbit is closed, such as an elliptical orbit. The kinetic and potential energies are
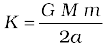
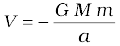
8. The escape speed from the surface of the earth is
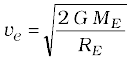 =
= 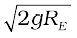
and has a value of 11.2 km s–1.
9. If a particle is outside a uniform spherical shell or solid sphere with a spherically symmetric internal mass distribution, the sphere attracts the particle as though the mass of the sphere or shell were concentrated at the centre of the sphere.
10. If a particle is inside a uniform spherical shell, the gravitational force on the particle is zero. If a particle is inside a homogeneous solid sphere, the force on the particle acts toward the centre of the sphere. This force is exerted by the spherical mass interior to the particle.
11. A geostationary (geosynchronous communication) satellite moves in a circular orbit in the equatorial plane at a approximate distance of 4.22 × 104 km from the earth’s centre.
1. In considering motion of an object under the gravitational influence of another object the following quantities are conserved:
(a) Angular momentum
(b) Total mechanical energy
Linear momentum is not conserved
2. Angular momentum conservation leads to Kepler’s second law. However, it is not special to the inverse square law of gravitation. It holds for any central force.
3. In Kepler’s third law (see Eq. (8.1) and T2 = KS R3. The constant KS is the same for all planets in circular orbits. This applies to satellites orbiting the Earth [(Eq. (8.38)].
4. An astronaut experiences weightlessness in a space satellite. This is not because the gravitational force is small at that location in space. It is because both the astronaut and the satellite are in “free fall” towards the Earth.
5. The gravitational potential energy associated with two particles separated by a distance r is given by
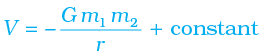
The constant can be given any value. The simplest choice is to take it to be zero. With this choice

This choice implies that V → 0 as r → ∞. Choosing location of zero of the gravitational energy is the same as choosing the arbitrary constant in the potential energy. Note that the gravitational force is not altered by the choice of this constant.
6. The total mechanical energy of an object is the sum of its kinetic energy (which is always positive) and the potential energy. Relative to infinity (i.e. if we presume that the potential energy of the object at infinity is zero), the gravitational potential energy of an object is negative. The total energy of a satellite is negative.
7. The commonly encountered expression m g h for the potential energy is actually an approximation to the difference in the gravitational potential energy discussed in the point 6, above.
8. Although the gravitational force between two particles is central, the force between two finite rigid bodies is not necessarily along the line joining their centre of mass. For a spherically symmetric body however the force on a particle external to the body is as if the mass is concentrated at the centre and this force is therefore central.
9. The gravitational force on a particle inside a spherical shell is zero. However, (unlike a metallic shell which shields electrical forces) the shell does not shield other bodies outside it from exerting gravitational forces on a particle inside. Gravitational shielding is not possible.
India has so far also launched 239 foreign satellites of 28 countries from Satish Dhawan Space Center, Sriharikota, Andhra Pradesh: May 26, 1999 (02); Oct. 22, 2001 (02); Jan. 10, 2007 (02); Apr. 23, 2007 (01); Jan. 21, 2008 (01); Apr. 28,2008 (08); Sep. 23,2009 (06); July 12, 2010 (03); Jan. 12,2011 (01); Apr. 20, 2011 (01) Sep. 09, 2012 (02); Feb. 25, 2013 (06); June 30, 2014 (05); July 10, 2015 (05); Sep. 28, 2015 (06); Dec. 16, 2015 (06); June 22, 2016 (17); Sep. 26, 2016 (05); Feb. 15, 2017 (101) and thus setting a world record; June 23, 2017 (29). Jan 12, 2018 (28); Sep. 16, 2018 (02).
Details can be seen at www.isro.gov.in.
a Launched from Kapustin Yar Missile and Space Complex, Soviet Union (now Russia)
b Launched from Satish Dhawan Space Centre, Sriharikota, Andhra Pradesh
c Launched from Centre Spatial Guyanais, Kourou, French Guiana
d Launched from Air Force Eastern Test Range, Florida
e Launched from Baikonur Cosmodrome, Kazakhstan
8.1 Answer the following :
(a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
(b) An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
(c) If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull. (you can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of sun. Why?
NEETprep Answer8.2 Choose the correct alternative :
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).
(c) Acceleration due to gravity is independent of the mass of the earth/mass of the body.
(d) The formula is more/less accurate than the formula
for the difference of potential energy between two points distance away from the center of the earth.
8.3 Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?
NEETprep Answer8.4 Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 108 m. Show that the mass of Jupiter is about one-thousandth that of the sun.
NEETprep Answer8.5 Let us assume that our galaxy consists of 2.5 × 1011 stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic center take to complete one revolution? Take the diameter of the Milky Way to be light years.
NEETprep Answer8.6 Choose the correct alternative:
(a) If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potential energy.
(b) The energy required to launch an orbiting satellite out of earth’s gravitational influence is more/less than the energy required to project a stationary object at the same height (as the satellite) out of earth’s influence.
NEETprep Answer8.7 Does the escape speed of a body from the earth depend on (a) the mass of the body, (b) the location from where it is projected, (c) the direction of projection, (d) the height of the location from where the body is launched?
NEETprep Answer8.8 A comet orbits the sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
NEETprep Answer8.9 Which of the following symptoms is likely to afflict an astronaut in space (a) swollen feet, (b) swollen face, (c) headache, (d) orientational problem.
NEETprep Answer8.10 In the following two exercises, choose the correct answer from among the given ones:
The gravitational intensity at the center of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b,(iii) c, (iv) o.
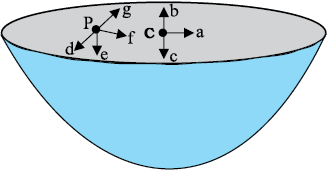
8.11 For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
NEETprep Answer8.12 A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2×1030 kg, mass of the earth = 6×1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
NEETprep Answer8.13 How will you weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
8.14 A Saturn year is 29.5 times the earth year. How far is Saturn from the sun if the earth is 1.50 × 108 km away from the sun?
NEETprep Answer8.15 A body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?
NEETprep Answer8.16 Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed 250 N on the surface?
NEETprep Answer8.17 A rocket is fired vertically with a speed of 5 km s-1 from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth = 6.0 × 1024 kg; mean radius of the earth = 6.4 × 106 m; G = 6.67 × 10–11 N m2 kg–2.
NEETprep Answer8.19 A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite = 200 kg; mass of the earth = 6.0×1024 kg; radius of the earth = 6.4 × 106 m; G = 6.67 × 10–11 N m2 kg-2.
NEETprep Answer8.20 Two stars each of one solar mass (= 2×1030 kg) are approaching each other for a head-on collision. When they are a distance 109 km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 104 km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
NEETprep Answer8.21 Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the midpoint of the line joining the centres of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?
NEETprep Answer8.22 As you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to the earth’s gravity at the site of this satellite? (Take the potential energy at infinity to be zero). Mass of the earth = 6.0×1024 kg, radius = 6400 km.
NEETprep Answer8.23 A star 2.5 times the mass of the sun and collapsed to a size of 12 km rotates with a speed of 1.2 rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity ? (mass of the sun = 2×1030 kg).
NEETprep Answer8.24 A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system? Mass of the space ship = 1000 kg; mass of the sun = 2×1030 kg; mass of mars = 6.4×1023 kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 ×108 km; G = 6.67×10-11 N m2 kg–2.
NEETprep Answer8.25 A rocket is fired ‘vertically’ from the surface of mars with a speed of 2 km s–1. If 20% of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it ? Mass of mars = 6.4×1023 kg; radius of mars = 3395 km; G = 6.67×10-11 N m2 kg–2.
Q. 1
The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth,
the acceleration due to gravity
(1) will be directed towards the centre but not the same everywhere
(2) will have the same value everywhere but not directed towards the centre
(3) will be same everywhere in magnitude directed towards the centre
(4) cannot be zero at any point
NEETprep AnswerQ. 2 As observed from the earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from the earth, this would
(a) be similarly true
(b) not be true because the force between the earth and mercury is not inverse square law
(c) not be true because the major gravitational force on mercury is due to the sun
(d) not be true because mercury is influenced by forces other than gravitational forces
NEETprep AnswerQ. 3 Different points in the earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigi body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the CM (centre of mass causing translation and a net torque at the CM causing rotation around ar axis through the CM. For the earth-sun system (approximating the earth as a uniform density sphere).
(a) the torque is zero
(b) the torque causes the earth to spin
(c)the rigid body result is not applicable since the earth is not even approximately a rigid body
(d) the torque causes the earth to move around the sun
NEETprep AnswerQ. 4 Satellites orbitting the earth have finite life and sometimes debris of satellites fall to the earth. This is because
(a) the solar cells and batteries in satellites run out
(b) the laws of gravitation predict a trajectory spiralling inwards
(c) of viscous forces causing the speed of satellite and hence height to gradually decrease
(d) of collisions with other satellites
NEETprep AnswerQ. 5 Both the earth and the moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon
(a) will be eilliptical
(b) will not be strictly elliptical because the total gravitational force on it is not central
(c) is not elliptical but will necessarily be a closed curve
(d) deviates considerably from being elliptical due to influence of planets other than the earth
NEETprep AnswerQ. 6 In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They
(a) will not move around the sun, since they have very small masses comparedto the sun
(b) will movein an irregular way because oftheir small masses andwill drift away into outer space
(c) will move around the sun in closed orbits but not obey Kepler’s laws
(d) will movein orbits like planets and obey Kepler’s laws
NEETprep AnswerQ. 7 Choose the wrong option.
(a) Inertial mass is a measure of difficulty of accelerating a body by an external force whereasthe gravitational massis relevant in determining the gravitational force on it by an external mass
(b) That the gravitational mass and inertial mass are equal is an experimental result
(c) That the acceleration due to gravity on the earth is the same forall bodies is due to the equality of gravitational mass and inertial mass
(d) Gravitational mass of a particle like proton can depend on the presence of neighbouring heavy objects but the inertial mass cannot
NEETprep AnswerQ. 8 Particles of masses 2M, m and M are respectively at points A, B and C with . m is much-much smaller than M and at time t = 0, they are all at rest as given in figure.
At subsequent times before anycollision takes place.
![]()
(a) m will remain at rest
(b) m will move towards M
(c) m will move towards 2M
(d) m will have oscillatory motion
NEETprep AnswerQ. 9 Which of the following options are correct?
(a) Acceleration due to gravity decreases with increasing altitude
(b) Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density)
(c) Acceleration due to gravity increases with increasing latitude
(d) Acceleration due to gravity is independent of the mass of the earth
NEETprep AnswerQ. 10 If the law of.gravitation, instead of being inverse square law, becomes an inverse cube law
(a) planets will not haveelliptic orbits
(b) circular orbits of planets is not possible
(c) projectile motion of a stone thrown by hand on the surface ofthe earth will be approximately parabolic
(d) there will be no gravitational force inside a spherical shell of uniform density
NEETprep AnswerQ. 11 If the mass of the sun were ten times smaller and gravitational constant G were ten times larger in magnitude. Then,
(a) walking on ground would become more difficult
(b) the acceleration due to gravity on the earth will not change
(c) raindrops will fall much faster
(d) airplanes will have to travel much faster
NEETprep AnswerQ. 12 If the sun and the planets carried huge amounts of opposite charges,
(a) all three of Kepler’s laws would still be valid
(b) only the third law will be valid
(c) the second law will not change
(d) the first law will still be valid
NEETprep AnswerQ. 13 There have been suggestions that the value of the gravitational G becomes smaller constant when considered over very large time Period (in billions of years) in the future. If that happens, for our earth,
(a) nothing will change
(b) we will become hotter after billions of years
(c) we will be going around but not strictly in closed orbits
(d) after sufficiently long time we will leave the solar system
NEETprep AnswerQ. 14 Supposing. Newton’s law of gravitation for gravitation between two masses forces and Mm, and at positions and read
When is a constant of dimension of mass and n is a number. In such a case,
(a) the acceleration due to gravity on the earth will be different for different objects
(b) none of the three laws of Kepler will be valid
(c) only the third law will become invalid
(d) for n negative, an object lighter than water will sink in water
NEETprep AnswerQ. 15 Which of the following are true?
(a) A polar satellite goes around the earth’s pole in north-south direction
(b) A geostationary satellite goes around the earth in east-west direction
(c) A geostationary satellite goes around the earth in west-east direction
(d) A polar satellite goes around the earth in east-west direction
NEETprep AnswerQ. 16 The centre of mass of an extended body on the surface of the earth and its centre of gravity
(a) are always at the same point for anysize of the body
(b) are alwaysat the samepoint only for spherical bodies
(c) can neverbe at the same point
(d) is close to each otherfor objects, say of sizes less than 100 m
(e) both can changeif the object is taken deepinside the earth
NEETprep AnswerQ. 17 17 Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
NEETprep AnswerQ. 18 Give one example each of central force and non-central force.
NEETprep AnswerQ. 19 Draw areal velocity versus time graph for mars.
NEETprep AnswerQ. 20 Whatis the direction of areal velocity of the earth around the sun?
NEETprep AnswerQ. 21 How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?
NEETprep AnswerQ. 22 Is it possible for a body to have inertia but no weight?
NEETprep AnswerQ. 23 We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of
nearby matter by putting it inside a hollow sphere or by some other means?
Q. 24 An astronaut inside a small spaceship orbitting around the earth cannot detect gravity. If the space station orbitting around the earth has a
large size, can he hope to detect gravity?
Q. 25 The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F versus r
graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Q. 26 Out of aphelion and perihelion, where is the speed of the earth more and why?
NEETprep AnswerQ. 27 7 Whatis the angle between the equatorial plane and the orbital plane of
(a) polar satellite?
(b) geostationary satellite?
NEETprep AnswerQ. 28 Mean solar day is the time interval between two successive noon when sun passes through zenith point (meridian). Sidereal day is the time interval between two successive transit of a distant star through the zenith point (meridian). By drawing appropriate diagram showing the earth’s spin and orbital motion, show that mean solar day is 4 min longer than the sidereal day. In other words, distant stars would rise 4 min early every successive day.
NEETprep AnswerQ. 29 Two identical heavy spheres are separated by a distance 10 times their radius. Will an object placed at the mid-point of the line joining their
centres be in stable equilibrium or unstable equilibrium? Give reason for your answer.
Q. 30 Show the nature of the following graph for a satellite orbitting the
(a) KE versus orbital radius R
(b) PE versus orbital radius R
(c) TE versus orbital radius R
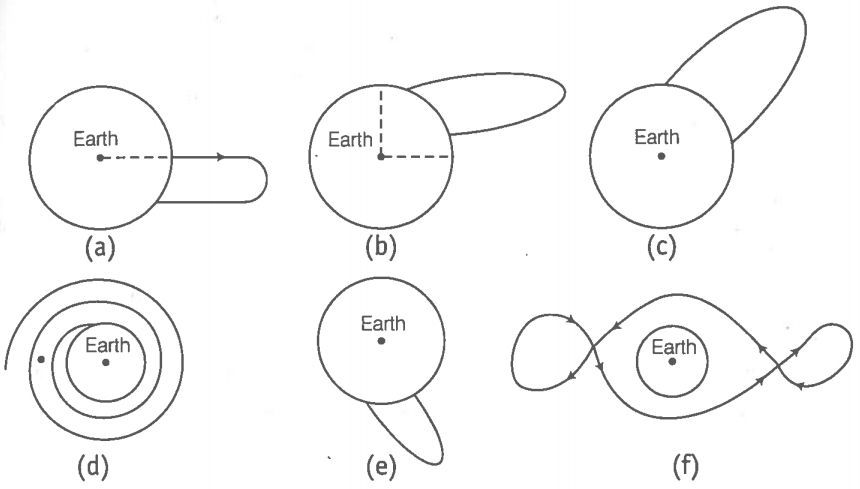
NEETprep AnswerQ. 31 Shown are several curves [fig. (a), (b), (c), (d), (e), (f)]. Explain with
reason, which ones amongst them can be possible trajectories traced by
a projectile (neglect air friction).
Q. 32 An object of mass m is raised from the surface of the earth to a heightequal to the radius of the earth, that is, taken from a distance R to 2R
from the centre of the earth. What is the gain in its potential energy?
Q. 33 A of mass m is placed at P a distance h along the normal through the centre 0 of a thin circular ring of mass M and radius r (figure).
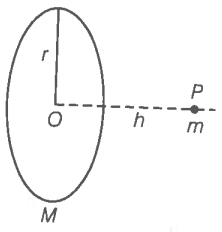
If the mass is moved further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h= r ?
NEETprep AnswerQ. 34 A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r
be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity , kinetic energy K, gravitational potential energy U, total energy & and angular momentum . As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
Q. 35 Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
NEETprep AnswerQ. 36 satellite is to be placed in equatorial geostationary orbit around the earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth, so that at least one satellite is visible from any point on the equator.
Q. 37 Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, the earth’ distance from the sun and Speed as it moves around the sun varies from day-to-day. This means that the length of the solar day is not constan) through the year. Assume that the earth's spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to non. Does this explain variation of length of the day during the year?
NEETprep AnswerQ. 38 A satellite is in an elliptic orbit around the earth with an aphelion of 6R and perihelion of 2R where R = 6400 km is the radius of the earth. Find
eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a
circular orbit of radius 6R?
SI unit and M= kg]
NEETprep Answer