(i) ${\left[Fe{\left(CN\right)}_6\right]}^{4-}$

 In the above coordination complex, iron exists in the +II oxidation state.
$F{e}^{2+}$ : Electronic configuration is as follows:

     Fe²⁺ = 3d⁶

As $C{N}^{-}$ is a strong field ligand, it causes the pairing of the unpaired 3d electrons.

Since there are six ligands around the central metal ion, the most feasible hybridization is $d^{2}s{p}^3 .$

6 electron pairs from CN^- ions occupy the six hybrid $d^{2}s{p}^3$
Then,

Hence, the geometry of the complex is octahedral and the complex is diamagnetic (as there are no unpaired electrons).

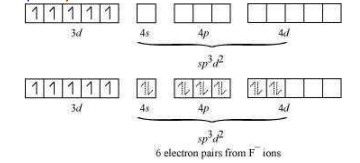
(ii) ${\left[Fe{F}_6\right]}^{3-}$

In this complex, the oxidation state of Fe is +3. The orbital diagram of Fe³⁺ is as follows: 
Fe³⁺ = 3d⁵ ; 

There are 6F^- ions. Thus, it will undergo $d^{2}s{p}^3$ or $s{p}^3{d}^2$ hybridization. As F^- is a weak field ligand, it does not cause the pairing of the electrons in the 3d orbital. Hence, the most feasible hybridization is $s{p}^3{d}^2$  

 $s{p}^3{d}^2$ hybridized orbitals of Fe are:

Hence, the geometry of the complex is found to be octahedral. 

(iii) [Co(C₂O₄)₃]^3–

Cobalt exists in the +3 oxidation state in the given complex.
The orbital diagram of Co³⁺ is as follows:

 Co³⁺ = 3d⁶ ; 

Oxalate is a weak field ligand. Therefore, it cannot cause the pairing of the 3d orbital electrons. Hence, the hybridization is sp³d²

Hence, the geometry of the complex is found to be octahedral.

(iv) [CoF₆]^3–

Cobalt exists in the +3 oxidation state. The orbital diagram of Co³⁺ is as follows:

Co³⁺ = 3d³;  

Again, the fluoride ion is a weak field ligand. It cannot cause the pairing of the 3d electrons. As a result, the Co³⁺ ion will undergo $s{p}^3{d}^2$ hybridization. 


Hence, the geometry of the complex is octahedral.