8.2 What are the oxidation number of the underlined elements in each of the following and how do you rationalise your results ?
(a) KI3 (b) H2S4O6 (c) Fe3O4 (d) CH3CH2OH (e) CH3COOH
(a) KI
In KI, the oxidation number (O.N.) of K is +1. Hence, the average oxidation number of I is . However, O.N. cannot be fractional. Therefore, we will have to consider the structure of KI to find the oxidation states. In a KI molecule, an atom of iodine forms a coordinate covalent bond with an iodine
molecule.
![]()
Hence, in a KI3 molecule, the O.N. of the two I atoms forming the I2 molecule is 0, whereas the O.N. of the I atom forming the coordinate bond is –1.
(b) HSO
![]()
Now, 2(+1)+4(x)+6(-2)=0
2+4x-12=0
4x=10
x=+2
However, O.N. cannot be fractional. Hence, S must be present in different oxidation states in the molecule.
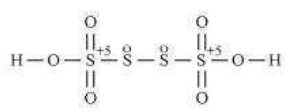
The O.N. of two of the four S atoms is +5 and the O.N. of the other two S atoms is 0.
(c)
On taking the O.N. of O as –2, the O.N. of Fe is found to be . However, O.N. cannot be fractional.
Here, one of the three Fe atoms exhibits the O.N. of +2 and the other two Fe atoms exhibit the O.N. of +3.
(d)
![]()
2(x)+4(+1)+1(-2)=0
2x+6-2=0
x=-2
Hence, the O.N. of C is –2.
(e)
![]()
2(x)+4(+1)+2(-2)=0
2x+4-4=0
x=0
However, 0 is average O.N. of C. The two carbon atoms present in this molecule are present in different environments. Hence, they cannot have the same oxidation number.
Thus, C exhibits the oxidation states of +2 and –2 in CH3COOH.
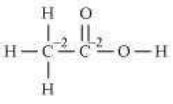

© 2026 GoodEd Technologies Pvt. Ltd.