(a) The O.N. (oxidation number) of P decreases from 0 in and increases from 0 in . Hence, acts both as an oxidizing agent and a reducing agent in this reaction.
Ion-electron method:
The oxidation half equation is:
The P atom is balanced as:
The O.N. is balanced by adding 8 electrons as:
The charge is balanced by adding as:
The H and O atoms are balanced by adding as:
The reduction half equation is:
The P atom is balanced as
The O.N. is balanced by adding 12 electrons as:
The charge is balanced by adding as:
The O and H atoms are balanced by adding as:
By muliplying equation (i) and 3 and (ii) with 2 and then adding them, the balanced chemical equation can be obtained as:
(b)
The oxidaion number of N increases from -2 in to +2 in NO and the oxidation number of Cl decreases from +5 in to -1 in . Hence, in this reaction, is the reducing agent and is the oxidizing agent.
Ion-electron method:
The oxidation half equation is:
The N atoms are balanced as:
The oxidation number is balanced by adding 8 electrons as :
The charge is balanced by adding 8 ions as:
The O atoms are balanced by adding as:
The reduction half equation is:
The oxidation number is balanced by adding 6 electrons as:
The charge is balanced by adding ions as:
The O atoms are balanced by adding as:
The balanced equation can be obtained by multiplying equation (i) with 3 and equation (ii) with 4 and then adding them as:
Oxidation number method:
Total decrease in oxidation number of N = 2 x 4 = 8
Total increase in oxidation number of Cl = 1 x 6 = 6
On multiplying with 3 and with 4 to balance the increase and decrease in O.N., we get:
The N and Cl atoms are balanced as:
The O atoms are balanced by adding as:
This is the required balanced equation.
(c)
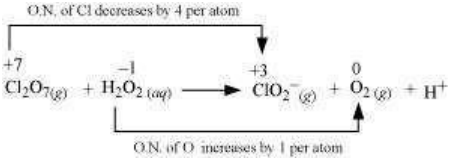
The oxidation number of Cl decreases from +7 in to +3 in and the oxidation number of O increases from -1 in to zero in . Hence, in this reaction, is the oxidizing agent and is the reducing agent.
Ion-electron method:
The oxidation half equation is:
The oxidation number is balanced by adding 2 electrons as:
The charge is balanced by adding ions as:
The oxygen atoms are balanced by adding as:
The reduction half equation is:
The Cl atoms are balanced as:
The oxidation number is balanced by adding 8 electrons as:
The charge is balanced by adding as:
The oxygen atoms are balanced by adding as:
The balanced equation can be obtained by multiplying the equation (i) with 4 and adding equation (ii) to its as:
Oxidation number method:
Total decrease in oxidation number of
Total increase in oxidation number of
By multiplying with 4 to balance the increase and decrease in the oxidation number, we get:
The Cl atoms are balanced as:
The O atoms are balanced by adding as:
The H atoms are balanced by adding as:
This is the required balanced equation.

