Ncert Exercises & Solutions

7.31 Dihydrogen gas used in Haber’s process is produced by reacting methane from natural gas with high-temperature steam. The first stage of the two-stage reaction involves the formation of CO and H2. In the second stage, CO formed in the first stage is reacted with more steam in water gas shift reaction,

CO (g) + H2O (g) 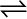CO2 (g) + H2 (g)

If a reaction vessel at 400°C is charged with an equimolar mixture of CO and steam such that $P_{CO} = P_{H_{2} O}$ = 4.0 bar, what will be the partial pressure of H2 at equilibrium? Kp= 10.1 at 400°C

Let the partial pressure of both carbon dioxide and hydrogen gas be p. The given reaction is:

${CO}_{(g)} + H_{2} O_{(g)} \leftrightarrow {CO}_{2 (g)} + H_{2 (g)}$
$Initial conc . 4.0 bar 4.0 bar 0 0$
$At equilibrium 4.0 - p 4.0 - p p p$
$It is given that K_{p} = 10.1 . \begin{aligned} \end{aligned}$

Now,

$\frac{p_{{co}_{2}} \times p_{H_{2}}}{p_{CO} \times p_{H_{2} O}} = K_{p} \Rightarrow \frac{p \times p}{(4.0 - p) (4.0 - p)} = 10.1 \Rightarrow \frac{p}{4.0 - p} = 3.178 \Rightarrow p = 12.712 - 3.178 p \Rightarrow 4.178 p = 12.178 p \Rightarrow p = 3.04$

Hence, at equilibrium, the partial pressure of $H_{2}$ will be 3.04 bar..

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions