5.40 A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for 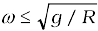 . What is the angle made by the radius vector joining the center to the bead with the vertically downward direction for
. What is the angle made by the radius vector joining the center to the bead with the vertically downward direction for 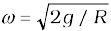 ? Neglect friction.
? Neglect friction.
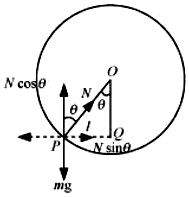
Let the angle made by the radius vector connecting the pellet to center of the ring be θ, with the vertical downward direction.
OP = R = Radius of the circle
N = Normal reaction
The respective vertical and horizontal equations of forces can be written as:
Mg = Ncosθ ………….. (i)
ml = Nsinθ ………... (ii)
In ΔOPQ, we have:
l = R sin θ ……………………… (iii)
Substituting equation (iii) in equation (ii), we get:
Substituting equation (iv) in equation (i), we get:
Since cosθ ≤ 1, the bead will remain at its lowermost point for
On equating equations (v) and (vi), we get:

© 2025 GoodEd Technologies Pvt. Ltd.