A train whistling at constant frequency is moving towards a station at a constant speed v. The train goes past a stationary observer on the station. The frequency n' of the sound as heard by the observer is plotted as a function of time t (figure). Identify the expected curve.
1. 2.
2. 
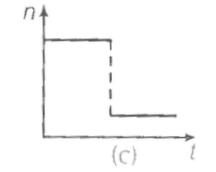 4.
4. 


© 2025 GoodEd Technologies Pvt. Ltd.