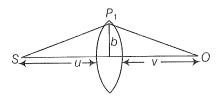
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as , where b is the verticle distance from the pole, is a constant. Using Fermat's principle i.e., the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the form
Show that an observer will see an image of a point object as a ring about the centre of the lens with an angular radius
Hint: Use Fermat's principle.
Step 1: Find the condition that all paraxial rays starting from the source will converge at a point O on the axis.
(i) The time elapsed to travel from S to is
or
The time required to travel from is,
The time required to travel through the lens is
where n is the refractive index.
Thus, the total time is
Put
Then,
Fermat's principle gives the time taken should be minimum.
For that first derivation should be zero,
Thus, a convergent lens is formed if . This is independent of B and hence, all paraxial rays from S will converge at O i.e., for rays
and (b<<v).
Since, , the focal length is D.
Step 2: Find the angular radius of the ring image.
(ii) In this case, differentiating expression of time taken t w.r.t. b;
Thus, all rays passing at a height b shall contribute to the image, The ray paths make an angle.
This is the required expression.

© 2026 GoodEd Technologies Pvt. Ltd.