Hint: The electromagnetic wave propagates perpendicular to both the electric field and the magnetic field.
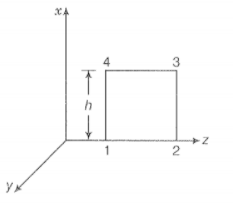
(I) Step 1: Consider the figure given below.
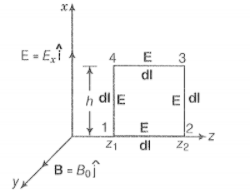
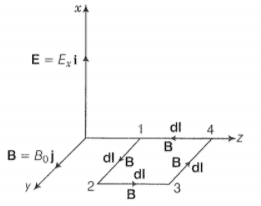
During the propagation of electromagnetic wave along z-axis, let electric field vector be along x-axis and magnetic field vector along the y-axis, i.e.,
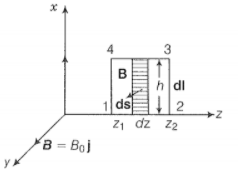
Line integral of over the closed rectangular path 1234 in the x-z plane of the figure;