Hint: Use the ampere-circuital law.
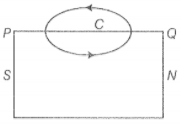
Step 1: Consider a magnetic field line of B through the bar magnet as given in the figure below.
The magnetic field line of B through the bar magnet must be a closed-loop.
Let C be the amperian loop. Then,
We know that the angle between B and dl is less than 90 inside the bar magnet. So, it is positive.
i.e.
Hence, the lines of B must run from the south pole (S) to the north pole (N) inside the bar magnet.
Step 2: According to Ampere's law,
As, (i.e., negative)
It will be so if the angle between H and dl is more than 90, so that cos is negative. It means the line of H must run from N-pole to S-pole inside the bar magnet.