(a)The theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

A physical body with center O and a point mass m, in the x–y plane at (x, y) is shown in the following figure.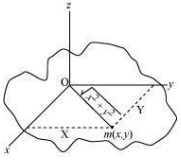

Moment of inertia about x-axis, Ix = mx2
Moment of inertia about y-axis, Iy = my2
Moment of inertia about z-axis, ${\mathrm{I}}_{\mathrm{z}}=\mathrm{m}(\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}{)}^2$
$\begin{array}{l}{\mathrm{I}}_{\mathrm{x}}+{\mathrm{I}}_{\mathrm{y}}={\mathrm{mx}}^2+{\mathrm{my}}^2\\ =\mathrm{m}({\mathrm{x}}^2+{\mathrm{y}}^2)\\ =\mathrm{m}(\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}{)}^2\end{array}$

$I_x+I_y=I_z$

Hence, the theorem is proved.

(b)The theorem of parallel axes states that the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its center of mass and the product of its mass and the square of the distance between the two parallel axes.

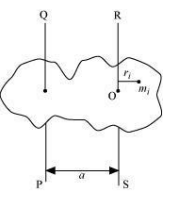
Suppose a rigid body is made up of n particles, having masses m1, m2, m3, … , mn, at perpendicular distances r1, r2, r3, … , rn respectively from the centre of mass O of the rigid body.

The moment of inertia about axis RS passing through the point O:

IRS = $\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{l}}{\mathrm{r}}_{\mathrm{i}}^2$

The perpendicular distance of mass mi, from the axis QP = a + ri

Hence, the moment of inertia about axis QP:

$\begin{array}{l}{\mathrm{I}}_{\mathrm{Or}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}(\mathrm{a}+{\mathrm{r}}_{\mathrm{i}}{)}^2\\ =\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}({\mathrm{a}}^2+{\mathrm{r}}_{\mathrm{i}}^2+2{\mathrm{ar}}_{\mathrm{i}}{)}^2\\ =\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{a}}^2+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{r}}_{\mathrm{i}}^2+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}2{\mathrm{ar}}_{\mathrm{i}}\\ ={\mathrm{I}}_{\mathrm{RS}}+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{a}}^2+2\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{ar}}_{\mathrm{i}}^2\end{array}$

Now, at the center of mass, the moment of inertia of all the particles about the axis passing through the center of mass is zero, that is,

$\begin{array}{l}2\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{ar}}_{\mathrm{i}}=0\\ \because \mathrm{a}\ne 0\\ \therefore \sum {\mathrm{m}}_{\mathrm{i}}{\mathrm{r}}_{\mathrm{i}}=0\\ \text{ Also, }\\ \sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{m}}_{\mathrm{i}}=\mathrm{M};\mathrm{M}=\text{ Total mass of the rigid body }\\ \therefore {\mathrm{I}}_{\mathrm{OP}}={\mathrm{I}}_{\mathrm{RS}}+{\mathrm{Ma}}^2\\ \text{ Hence, the theorem is proved. }\end{array}$