A man weighing 80 kg is standing in a trolley weighing 320 kg. The trolley is resting on frictionless horizontal rails. If the man starts walking on the trolley with a speed of 1 m/s, then after 4 sec his displacement relative to the ground will be

1. 5  m

2. 4.8 m

3. 3.2 m

4. 3.0 m

Six particles situated at the corners of a regular hexagon of side \(a\) move at constant speed \(v\). Each particle maintains a direction towards the particle at the next. The time which the particles will take to meet each other is:
1. \(\frac{2 a}{v}~\text{sec}\)
2. \(\frac{a}{v}~\text{sec}\)
3. \(\frac{2 a}{3v}~\text{sec}\)
4. \(\frac{3 a}{v}~\text{sec}\)

A ship A is moving westwards with a speed of 10 km ${\mathrm{h}}^{-1}$ and a ship B, 100 km south of A is moving northwards with a speed of 10 km ${\mathrm{h}}^{-1}$. The time after which the distance between them becomes the shortest, is:

1. 5 hr

2. $5\sqrt{2}$ hr

3. $10\sqrt{2}$ hr

4. 0 hr

A river is flowing with a speed of 1 km/hr. A swimmer wants to go to point 'C' starting from 'A'. He swims with a speed of 5 km/hr, at an angle $\theta$ with respect to the river. If \(\text {AB = BC = 400 m}\). Then

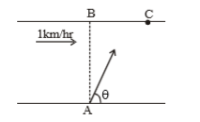
1. The time taken by the man is 12 min

2. The time taken by the man is 8 min

3. The value of $\theta$ is 45$°$

4. The value of $\theta$ is 53$°$

Two men \(P\) and \(Q\) are standing at corners \(A\) and \(B\) of a square \(ABCD\) of side \(8~\text m.\) They start moving along the track with a constant speed \(2~\text{m/s}\) and \(10~\text {m/s}\) respectively. The time when they will meet for the first time is equal to:
       
1. \(2~\text{sec}\)
2. \(3~\text{sec}\)
3. \(1~\text{sec}\)
4. \(6~\text{sec}\) 

A boat is sent across a river in perpendicular direction with a velocity of 8 km/hr. If the resultant velocity of boat is 10 km/hr, then velocity of the river is : 

1. 10 km/hr

2. 8 km/hr

3. 6 km/hr

4. 4 km/hr

A boat is moving with velocity of $3\hat{i}+4\hat{j}$ in river and water is moving with a velocity of $-3\hat{i}-4\hat{j}$ with respect to ground. Relative velocity of boat with respect to water is: 

1. $-6\hat{i}-8\hat{j}$

2. $6\hat{i}+8\hat{j}$

3. $8\hat{j}$

4. $6\hat{i}$

A boat moves with a speed of 5 km/h relative to water in a river flowing with a speed of 3 km/h and having a width of 1 km. The minimum time taken around a round trip(returning to the initial point) is:

1. 5 min

2. 60 min

3. 20 min

4. 30 min

A river is flowing from W to E with a speed of 5 m/min. A man can swim in still water with a velocity 10 m/min. In which direction should the man swim so as to take the shortest possible path to go to the south. 

1. 30° with downstream

2. 60° with downstream

3. 120° with downstream

4. South

A train is moving towards the east and a car is along the north at the same speed. The observed direction of the car to the passenger on the train is: