- 1(current)
Q. No.A wire carrying a current \(I_0\) oriented along the vector \(\big(3\hat{i}+4\hat{j}\big)\) experiences a force per unit length of \(\big(4F\hat{i}-3F\hat{j}-F\hat{k}\big).\) The magnetic field \(\vec{ B}\) equals:
1. \(\dfrac{F}{I_0}\left(\hat{i}+\hat{j}\right)\)
2. \(\dfrac{5F}{I_0}\left(\hat{i}+\hat{j}+\hat{k}\right)\)
3. \(\dfrac{F}{I_0}\left(\hat{i}+\hat{j}+\hat{k}\right)\)
4. \(\dfrac{5F}{I_0}\hat{k}\)
| 1. | \(q\Phi\) | 2. | \(\dfrac{q\Phi}{2\pi}\) |
| 3. | \(\pi q\Phi\) | 4. | \(\dfrac{q\Phi}{\pi}\) |
An electron enters a chamber in which a uniform magnetic field is present as shown.
An electric field of appropriate magnitude is also applied so that the electron travels undeviated without any change in its speed through the chamber. We are ignoring gravity. Then, the direction of the electric field is:
| 1. | opposite to the direction of the magnetic field. |
| 2. | opposite to the direction of the electron's motion. |
| 3. | normal to the plane of the paper and coming out of the plane of the paper. |
| 4. | normal to the plane of the paper and into the plane of the paper. |
A horizontal wire is placed in a uniform magnetic field directed vertically downward.
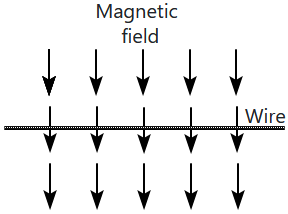
If an external force pulls the wire straight down along the page, which of the following best describes the magnetic force acting on the electrons in the wire?
1. Up.
2. Into the page.
3. Out of the page.
4. There is no magnetic force.
| Assertion (A): | Work done by magnetic force on a charged particle moving in a uniform magnetic field is zero. |
| Reason (R): | Path of a charged particle in a uniform magnetic field, projected in the direction of field, will be a straight line. |
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | Both (A) and (R) are false. |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.