Q. No.A particle is executing a simple harmonic motion. Its maximum acceleration is and maximum velocity is . Then its time period of vibration will be:
| 1. | \(\frac {\beta^2}{\alpha^2}\) | 2. | \(\frac {\beta}{\alpha}\) |
| 3. | \(\frac {\beta^2}{\alpha}\) | 4. | \(\frac {2\pi \beta}{\alpha}\) |
When two displacements are represented by \(y_1 = a \text{sin}(\omega t)\) and \(y_2 = b\text{cos}(\omega t)\) are superimposed, then the motion is:
| 1. | not simple harmonic. |
| 2. | simple harmonic with amplitude \(\frac{a}{b}\). |
| 3. | simple harmonic with amplitude \(\sqrt{a^2+b^{2}}.\) |
| 4. | simple harmonic with amplitude \(\frac{a+b}{2}\). |
A particle is executing SHM along a straight line. Its velocities at distances \(x_1\) and \(x_2\) from the mean position are \(v_1\) and \(v_2\), respectively. Its time period is:
| 1. | \(2 \pi \sqrt{\dfrac{x_{1}^{2}+x_{2}^{2}}{v_{1}^{2}+v_{2}^{2}}}~\) | 2. | \(2 \pi \sqrt{\dfrac{{x}_{2}^{2}-{x}_{1}^{2}}{{v}_{1}^{2}-{v}_{2}^{2}}}\) |
| 3. | \(2 \pi \sqrt{\dfrac{v_{1}^{2}+v_{2}^{2}}{x_{1}^{2}+x_{2}^{2}}}\) | 4. | \(2 \pi \sqrt{\dfrac{v_{1}^{2}-v_{2}^{2}}{x_{1}^{2}-x_{2}^{2}}}\) |
The oscillation of a body on a smooth horizontal surface is represented by the equation, \(X=A \text{cos}(\omega t)\),
where \(X=\) displacement at time \(t,\) \(\omega=\) frequency of oscillation.
Which one of the following graphs correctly shows the variation of acceleration, \(a\) with time, \(t?\)
(\(T=\) time period)
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | circle |
| 2. | hyperbola |
| 3. | ellipse |
| 4. | a straight line passing through the origin |
1. Only (IV) does not represent SHM
2. (I) and (III)
3. (I) and (II)
4. Only (I)
A particle of mass \(m\) is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
| 1. |  |
2. |  |
| 3. |  |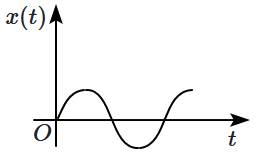
4. |  |
1. \(\frac{\pi}{6}\)
2. \(0\)
3. \(\frac{2\pi}{3}\)
4. \(\pi\)
The displacement of a particle along the x-axis is given by, x = asin2t. The motion of the particle corresponds to:
| 1. | simple harmonic motion of frequency |
| 2. | simple harmonic motion of frequency |
| 3. | non-simple harmonic motion |
| 4. | simple harmonic motion of frequency |
1. \(T\)
2. \(\frac{T}{\sqrt{2}}\)
3. \(2T\)
4. \(\sqrt{2}T\)
© 2025 GoodEd Technologies Pvt. Ltd.