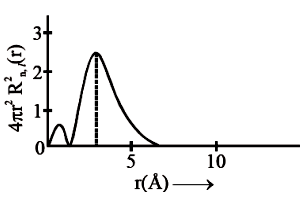
The graph between ${\left|\psi \right|}^2$ and r (radial distance) is shown below. This represents:

1.	3s orbital	2.	2s orbital
3.	2p orbital	4.	1s orbital

A proton and a Li³⁺ nucleus are accelerated by the same potential. If $\lambda$_Li³⁺ and ${\lambda }_p$ denote the de-Broglie wavelengths of Li³⁺ and proton respectively, then the value of \(\frac{\lambda _{Li^{3+}}}{\lambda _{p}}\) is x × 10⁻¹. The value of x is:

(Rounded off to the nearest integer)

(Mass of Li³⁺ = 8.3 the mass of a proton) 

1. 4 
2. 6 
3. 2
4. 8
 

According to Bohr's atomic theory:

Choose the most appropriate answer from the options given below :

1. (C) Only

2. (A) Only

3. (A), (C) and (D) only

4. (A) and (D) only

The plots of radial distribution functions for various orbitals of hydrogen atom against 'r' are given below:

a.

b.

c. 

d.

The correct plot for 3s orbital is:

1. (B)

2. (A)

3. (D)

4. (C)

The radius of the second Bohr orbit for hydrogen atom is:

(Planck's Const. h = 6.6262 × 10^–34 Js; mass of electron = 9.1091 × 10^–31 kg; charge of electron e = 1.60210 ×10^–19 C; permittivity of vaccum ∈₀ = 8.854185 ×10^–12 kg^–1m^–3A²)

1. 0.529 Å

2. 2.12 Å

3. 1.65 Å

4. 7.76 Å

The electrons identified by quantum numbers n and l can be placed in order of increasing energy as:

a. n = 4, $\mathcal{l}$ = 1

b. n = 4, $\mathcal{l}$ = 0

c. n = 3, $\mathcal{l}$ = 2

d. n = 3, $\mathcal{l }$= 1

The correct set of four quantum numbers for the valence electrons of rubidium atom (Z = 37) is -

1. 5, 1, 0 + $\frac{1}{2}$

2. 5, 1, 1 + $\frac{1}{2}$

3. 5, 0, 1 +$\frac{1}{2}$

4. 5, 0, 0 + $\frac{1}{2}$

The energy of an electron is given by E = – 2.178 × ${10}^{-18}\mathrm{J}\left(\frac{{\displaystyle {\mathrm{Z}}^2}}{{\displaystyle {\mathrm{n}}^2}}\right)$ Wavelength of light required to excite an electron in an hydrogen atom from level n = 1 to n = 2 will be:
(h = 6.62 × 10–³⁴ Js and c = 3.0 × 10⁸ ms^–1)

1. 6.500 × 10^–7 m

2. 8.500 × 10^–7 m

3. 1.214 × 10^–7 m

4. 2.816 × 10^–7 m

A gas absorbs a photon of 355 nm and emits at two wavelengths. If one of the emissions is at 680 nm, the other is at:

1. 1035 nm

2. 325 nm

3. 743 nm

4. 518 nm

The energy required to break one mole of CI–Cl bonds in Cl₂ is 242 kJmol⁻¹. The wavelength of light capable of breaking a single Cl–Cl bond is:$\mathrm{}\mathrm{}\mathrm{}{\mathrm{}}^{\mathrm{}}{}^{\mathrm{}}{\mathrm{}}_{\mathrm{}}$

1. 494 nm

2. 594 nm

3. 640 nm

4. 700 nm