Select Chapter Topics:
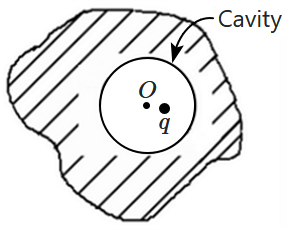
Q. No.A point charge \(q\) is placed within a spherical cavity inside a metallic conductor, slightly off-centre. The charge \(q\) induces a charge distribution on the inner surface of the cavity. The net force on \(q\) due to the induced charges is:
| 1. | zero |
| 2. | towards the centre |
| 3. | away from the centre |
| 4. | either towards or away from the centre depending on the sign of \(q\) |
Subtopic: Gauss's Law |
Level 4: Below 35%
Hints
Given below are two statements:
| Assertion (A): | The electrostatic field of a charge distributed uniformly over the surface of a sphere vanishes within the sphere, only at its centre. |
| Reason (R): | This cancellation occurs at the centre due to the symmetry of the sphere and the symmetric, uniform charge distribution. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | (A) is False but (R) is True. |
Subtopic: Electric Field |
Level 3: 35%-60%
Hints
An electric field is given by: \(\vec{E}(x,~y)=4 x \hat{\imath}-3 y \hat{\jmath}\); the field being measured in \(\text{'V/m'}\) and the distances in \(\text{'m'}.\) The variation of the potential along the direction \((\hat i - \hat j)\) at the point \((2, 2)\) is given by:
1. \(-14 ~\text{V/m}\)
2. \(14 ~\text{V/m}\)
3. -\(7 \sqrt 2~\text{V/m}\)
4. \(7 \sqrt 2~\text{V/m}\)
1. \(-14 ~\text{V/m}\)
2. \(14 ~\text{V/m}\)
3. -\(7 \sqrt 2~\text{V/m}\)
4. \(7 \sqrt 2~\text{V/m}\)
Subtopic: Electric Field |
Level 3: 35%-60%
Please attempt this question first.
Hints
Please attempt this question first.
Which of the following field configurations is/are possible?
Note: \(A,B,C\) are conductors. Other charges may be present in the vicinity.
Note: \(A,B,C\) are conductors. Other charges may be present in the vicinity.
| 1. | I, III | 2. | II |
| 3. | I, II, III | 4. | none of I, II, III |
Subtopic: Electric Field |
Level 3: 35%-60%
Hints
Three identical charges (\(q\) each) are placed at the three vertices \(A,B,C\) of an equilateral triangle of side \(a.\) Let \(O\) be the centre (centroid) of the triangle \(ABC\) and \(O'\) be the reflection of \(O\) in \(BC.\) The electric field at \(O,\) due to any one of the charges, is \(E.\) The net field at \(O',\) due to all the three charges, is:
| 1. | \(2E\) | 2. | \(\Large\frac{3E}{2}\) |
| 3. | \(\Large\frac{4E}{3}\) | 4. | \(\Large\frac{5E}{4}\) |
Subtopic: Electric Field |
Level 3: 35%-60%
Hints
Equal and opposite charges are placed at the two vertices of an equilateral triangle, giving a dipole moment \(p.\) A small dipole \(p'\) is placed at the third vertex, parallel to the previous dipole. If the electric fields due to both dipoles \(p,~p',\) at the mid-point of the dipole \(p,\) are equal, then \(\dfrac{p'}{p}\) equals:
| 1. | \(3\sqrt3\) | 2. | \(\dfrac{3\sqrt3}{2}\) |
| 3. | \(\sqrt3\) | 4. | \(\dfrac{\sqrt3}{2}\) |
Subtopic: Electric Dipole |
Level 3: 35%-60%
Hints
Two identical balls of cork \(\mathrm{(C_1,C_2)}\) are charged oppositely with equal amounts of charge distributed uniformly over their respective surfaces. Two similar (of same size) balls of copper\((M_1,M_2)\) are charged in the same way as the previous two balls. \(\mathrm{C_1,C_2}\) are allowed to touch each other briefly and are separated, and the same is done with \(M_1,M_2.\) The electrostatic force between \(\mathrm{C_1,C_2}\) is \(F_C\) and that between \(M_1,M_2\) is \(F_M\) at the same separation. Then:
| 1. | \(F_C=0,F_M\neq0\) | 2. | \(F_C\neq0,F_M=0\) |
| 3. | \(F_C=0,F_M=0\) | 4. | \(F_C\neq0,F_M\neq0\) |
Subtopic: Electric Charge |
Level 3: 35%-60%
Hints
A dipole is placed at the centre of a uniformly charged circular ring, with the axis of the dipole along the axis of the ring.
The dipole experiences:
1. no force and no torque.
2. a force but no torque.
3. a torque but no force.
4. a force and a torque.
The dipole experiences:
1. no force and no torque.
2. a force but no torque.
3. a torque but no force.
4. a force and a torque.
Subtopic: Electric Dipole |
Level 3: 35%-60%
Hints
A thin uniform rod of mass \(M\) and length \(L\) is suspended from one of its ends, '\(A\)', so that it can rotate freely about it. A charge '\(q\)' is fixed to its lower end \(B\). A uniform horizontal Electric field is switched on and the rod rotates about \(A\), finally coming to equilibrium – making an angle of \(45^{\circ}\) with the vertical. If the acceleration due to gravity is '\(g\)', then,
1. \(qE =Mg\)
2. \(2qE =Mg\)
3. \(qE =2Mg\)
4. \(\sqrt{2}qE =Mg\)
1. \(qE =Mg\)
2. \(2qE =Mg\)
3. \(qE =2Mg\)
4. \(\sqrt{2}qE =Mg\)
Subtopic: Electric Field |
Level 3: 35%-60%
Hints
Two infinite line charges, carrying charges \(+\lambda,-\lambda\) (per unit length) are placed parallel to each other, a short distance \(a\) apart. The electric field at a distance r from one of the charges \((A P = r)\) is:
| 1. | constant | 2. | proportional to \(\dfrac{1}{r}\) |
| 3. | proportional to \(\dfrac{1}{r^2}\) | 4. | proportional to \(\dfrac{1}{r^3}\) |
Subtopic: Electric Field |
Level 3: 35%-60%
Hints
Select Chapter Topics:
© 2025 GoodEd Technologies Pvt. Ltd.