The value of \(M\), as shown, for which the rod will be in equilibrium is:
| 1. | \(1\) kg | 2. | \(2\) kg |
| 3. | \(4\) kg | 4. | \(6\) kg |
In the figure given below, \(O\) is the centre of an equilateral triangle \(ABC\) and \(\vec{F_{1}} ,\vec F_{2}, \vec F_{3}\) are three forces acting along the sides \(AB\), \(BC\) and \(AC\). What should be the magnitude of \(\vec{F_{3}}\) so that total torque about \(O\) is zero?
1. \(\left|\vec{F_{3}}\right|= \left|\vec{F_{1}}\right|+\left|\vec{F_{2}}\right|\)
2. \(\left|\vec{F_{3}}\right|= \left|\vec{F_{1}}\right|-\left|\vec{F_{2}}\right|\)
3. \(\left|\vec{F_{3}}\right|= \vec{F_{1}}+2\vec{F_{2}}\)
4. Not possible
A force \(\vec{F}=\hat{i}+2\hat{j}+3\hat{k}~\text{N}\) acts at a point \(\hat{4i}+3\hat{j}-\hat{k}~\text{m}\). Let the magnitude of the torque about the point \(\hat{i}+2\hat{j}+\hat{k}~\text{m}\) be \(\sqrt{x}~\text{N-m}\). The value of \(x\) is:
1. \(145\)
2. \(195\)
3. \(245\)
4. \(295\)
A wheel with a radius of \(20\) cm has forces applied to it as shown in the figure. The torque produced by the forces of \(4\) N at \(A\), \(8~\)N at \(B\), \(6\) N at \(C\), and \(9~\)N at \(D\), at the angles indicated, is:
1. \(5.4\) N-m anticlockwise
2. \(1.80\) N-m clockwise
3. \(2.0\) N-m clockwise
4. \(3.6\) N-m clockwise
Which of the following is the value of the torque of force \(F\) about origin \(O:\)
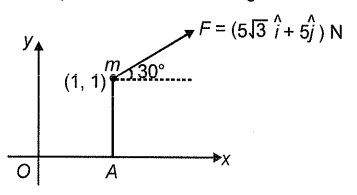
1. \(\vec{\tau}=5(1-\sqrt{3}) \hat{k}\) N-m
2. \(\vec{\tau}=5(1-\sqrt{3}) \hat{j}\) N-m
3. \(\vec{\tau}=5(\sqrt{3}-1) \hat{i}\) N-m
4. \(\vec{\tau}=\sqrt{3} \hat{j}\) N-m
| 1. | \(\vec{\tau}=(-17 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+4 \widehat{\mathrm{k}})\) N-m |
| 2. | \(\vec{\tau}=(-17 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}-4 \widehat{\mathrm{k}}) \) N-m |
| 3. | \(\vec{\tau}=(17 \hat{\mathrm{i}}-6 \hat{\mathrm{j}}+4 \widehat{\mathrm{k}})\) N-m |
| 4. | \(\vec{\tau}=(-41 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+16 \hat{\mathrm{k}})\) N-m |
Shown in the figure is a rigid and uniform one-metre long rod, \(AB\), held in the horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass \(m\) and has another weight of mass \(2m\) hung at a distance of \(75\) cm from \(A\). The tension in the string at \(A\) is:

1. \(2mg\)
2. \(0.5mg\)
3. \(0.75mg\)
4. \(1mg\)
| 1. | \(wx \over d\) | 2. | \(wd \over x\) |
| 3. | \(w(d-x) \over x\) | 4. | \(w(d-x) \over d\) |
For \(L = 3.0~\text{m,}\) the total torque about pivot \(A\) provided by the forces as shown in the figure is:

| 1. | \(210 ~\text{Nm}\) | 2. | \(140 ~\text{Nm}\) |
| 3. | \(95 ~\text{Nm}\) | 4. | \(75 ~\text{Nm}\) |
A body of mass M is moving on a circular track of radius r in such a way that its kinetic energy K depends on the distance travelled by the body s according to relation K = s, where is a constant. The angular acceleration of the body is:
1.
2.
3.
4.







