The relation between two specific heats (in cal/mol) of a gas is:
1.
2.
3.
4.
The ratio of the specific heats \(\frac{C_P}{C_V}=\gamma\) in terms of degrees of freedom \((n)\) is given by:
1. \(1+1/n\)
2. \(1+n/3\)
3. \(1+2/n\)
4. \(1+n/2\)
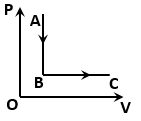
The figure shows a process for a gas in which pressure (P) and volume (V) of the gas change. If and are the molar heat capacities of the gas during the processes AB and BC respectively, then:
1.
2.
3.
4.
The specific heat of an ideal gas is:
1. proportional to
2. proportional to T2.
3. proportional to T3.
4. independent of
For hydrogen gas, the difference between molar specific heats is given by; \(C_P-C_V=a,\) and for oxygen gas, \(C_P-C_V=b.\) Here, \(C_P\) and \(C_V\) are molar specific heats expressed in \(\text{J mol}^{-1}\text{K}^{-1}.\) What is the relationship between \(a\) and \(b?\)
1. \(a=16b\)
2. \(b=16a\)
3. \(a=4b\)
4. \(a=b\)