Q. No.A copper rod of \(88\) cm and an aluminium rod of an unknown length have an equal increase in their lengths independent of an increase in temperature. The length of the aluminium rod is:
\(\left(\alpha_{Cu}= 1.7\times10^{-5}~\text{K}^{-1}~\text{and}~\alpha_{Al}= 2.2\times10^{-5}~\text{K}^{-1}\right)\)
| 1. | \(68~\text{cm}\) | 2. | \(6.8~\text{cm}\) |
| 3. | \(113.9~\text{cm}\) | 4. | \(88~\text{cm}\) |
| 1. | \(\alpha_1L_2^2=\alpha_2L_1^2\) | 2. | \(\alpha_1^2L_2=\alpha_2^2L_1\) |
| 3. | \(\alpha_1L_1=\alpha_2L_2\) | 4. | \(\alpha_1L_2=\alpha_2L_1\) |
The value of the coefficient of volume expansion of glycerine is \(5\times10^{-4}~\text{K}^{-1}.\) The fractional change in the density of glycerine for a rise of \(40^\circ \text{C}\) in its temperature is:
| 1. | \(0.015\) | 2. | \(0.020\) |
| 3. | \(0.025\) | 4. | \(0.010\) |
| 1. | \(3 \times 10^{-4} / ^\circ\text C\) | 2. | \(2 \times 10^{-4} / ^\circ\text C\) |
| 3. | \(6 \times 10^{-4} / ^\circ\text C\) | 4. | \(10^{-4} / ^\circ\text C\) |
| 1. | \(50 \times 10^3~ \text N\) | 2. | \(100 \times 10^3 ~\text N\) |
| 3. | \(2 \times 10^3~\text N\) | 4. | \(5 \times 10^3 ~\text N\) |
Two identical bodies are made of a material for which the heat capacity increases with temperature. One of these is at \(100~^{\circ}\text{C},\) while the other one is at \(0~^{\circ}\text{C}.\) If the two bodies are brought into contact, then assuming no heat loss, the final common temperature is:
| 1. | \(50~^{\circ}\text{C}\) |
| 2. | more than \(50~^{\circ}\text{C}\) |
| 3. | less than \(50~^{\circ}\text{C}\) but greater than \(0~^{\circ}\text{C}\) |
| 4. | \(0~^{\circ}\text{C}\) |
[Latent heat of ice is \(3.4 \times 10^5~\text{J/kg}\) and \(g=10~\text{N/kg}\)]
| 1. | \(544~\text{km}\) | 2. | \(136~\text{km}\) |
| 3. | \(68~\text{km}\) | 4. | \(34~\text{km}\) |
[Take specific heat of water \(= 1~\text{cal g}^{-1}~^\circ\text{C}^{-1}\) and latent heat of steam \(= 540~\text{cal g}^{-1}\)]
| 1. | \(24~\text{g}\) | 2. | \(31.5~\text{g}\) |
| 3. | \(42.5~\text{g}\) | 4. | \(22.5~\text{g}\) |
Liquid oxygen at \(50~\text K\) is heated up to \(300~\text K\) at a constant pressure of \(1~\text{atm}.\) The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?
| 1. |  |
2. |  |
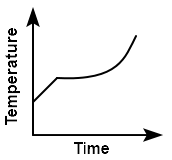| 3. |  |
4. |  |
| 1. | \(\dfrac{5}{3}\) | 2. | \(\dfrac{5}{4}\) |
| 3. | \(\dfrac{3}{2}\) | 4. | \(\dfrac{4}{3}\) |
© 2025 GoodEd Technologies Pvt. Ltd.