An LED is constructed from a \(\mathrm{p\text{-}n}\) junction diode using \(\mathrm{GaAsP}.\) The energy gap is \(1.9~\text{eV}.\) The wavelength of the light emitted will be equal to:
1. \(10.4 \times 10^{-26}~ \text{m}\)
2. \(654~ \text{nm}\)
3. \(654~ \text{m}\)
4. \(654\times 10^{-11}~\text{m}\)
1. \(10.4 \times 10^{-26}~ \text{m}\)
2. \(654~ \text{nm}\)
3. \(654~ \text{m}\)
4. \(654\times 10^{-11}~\text{m}\)
| 1. | \(1.0 \times 10^6 ~\text{V/m}\) | 2. | \(1.0 \times 10^5 ~\text{V/m}\) |
| 3. | \(2.0 \times 10^5 ~\text{V/m}\) | 4. | \(2.0 \times 10^6 ~\text{V/m}\) |

| 1. | \(5~\text A\) | 2. | \(0.2~\text A\) |
| 3. | \(0.6~\text A\) | 4. | zero |
| 1. | \(V_B\) increases, \(x\) decreases | 2. | \(V_B\) decreases, \(x\) increases |
| 3. | \(V_B\) increases, \(x\) increases | 4. | \(V_B\) decreases, \(x\) decreases |
If the reverse bias in a junction diode is changed from \(5~\text V\) to \(15~\text V\) then the value of current changes from \(38~\mu \text{A}\) to \(88~\mu \text{A}.\) The resistance of the junction diode will be:
1. \(4\times10^{5}\)
2. \(3\times10^{5}\)
3. \(2\times10^{5}\)
4. \(10^{6}\)
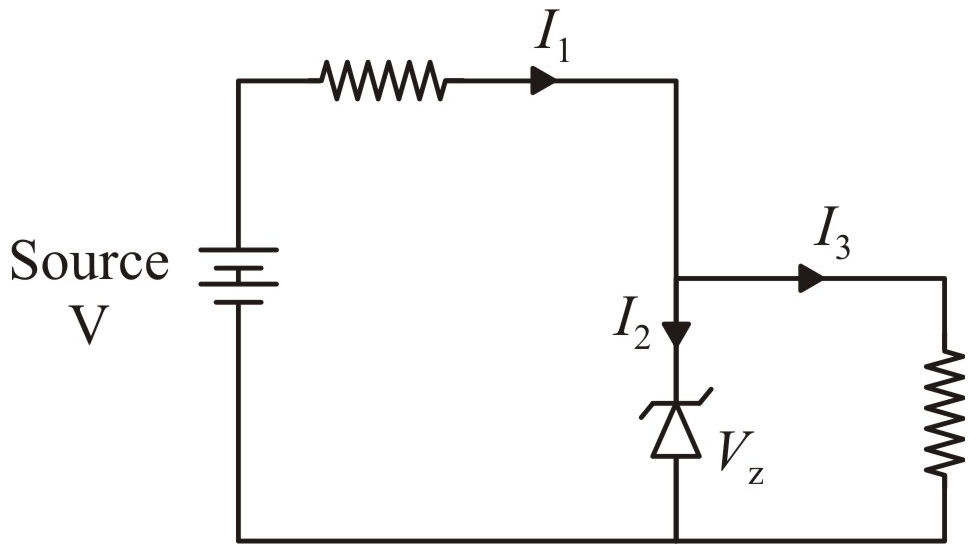
A Zener diode is shown in the following circuit diagram. When the source voltage fluctuates such that \(V>V_z\) then:
| 1. | all the current \(I_1, I_2~\text{and}~I_3\) change. |
| 2. | only \(I_1\) and \(I_2\) change and \(I_3\) remains constant. |
| 3. | only \(I_1\) and \(I_3\) change and \(I_2\) remains constant. |
| 4. | all the currents remain constant. |

| 1. | \(2~\text A\) and zero | 2. | \(3~\text A\) and \(2~\text A\) |
| 3. | \(2~\text A\) and \(3~\text A\) | 4. | Zero and \(2~\text A\) |
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The combination of gates shown in the diagram is equivalent to:
1. OR
2. AND
3. NAND
4. NOT
A Zener diode is used to obtain a constant voltage. If the applied voltage \(V\) changes, then:
(\( V\) is more than Zener voltage)

| 1. | \(i_{1}\) and \(i_{2}\) change. |
| 2. | \(i_{2}\) and \( V_{0}\) change and \(i_{3}\) remain constant. |
| 3. | \(i_{2}\) and \(V_{0}\) don't change while \(i_{3}\) changes. |
| 4. | \(i_{3}\) and \( V_{0}\) don't change while \(i_{2}\) changes. |