An object is placed \(20\) cm in front of a concave mirror of a radius of curvature \(10\) cm. The position of the image from the pole of the mirror is:
1. \(7.67\) cm
2. \(6.67\) cm
3. \(8.67\) cm
4. \(9.67\) cm
1. \(7.67\) cm
2. \(6.67\) cm
3. \(8.67\) cm
4. \(9.67\) cm
The angle of minimum deviation for a glass prism of refractive index \(\mu = \sqrt{3}\) equals the refracting angle of the prism. The angle of the prism is:
1. \(30^{\circ}\)
2. \(60^{\circ}\)
3. \(90^{\circ}\)
4. \(45^{\circ}\)
The angle of a prism is \(A\) and one of its refracting surfaces is silvered. Light rays falling at an angle of incidence \(2A\) on the first surface return through the same path after suffering reflection at the second (silvered) surface. The refractive index of the material is:
1. \(2\sin{A}\)
2. \(2\cos{A}\)
3. \(\frac{1}{2}\cos{A}\)
4. \(\tan{A}\)
The correct statement is:
| 1. | The intermediate image in a compound microscope is real, erect and magnified |
| 2. | Intermediate image in a compound microscope is real, inverted, but diminished |
| 3. | Intermediate image in a compound microscope is virtual, erect and magnified |
| 4. | Intermediate image in a compound microscope is real, inverted and magnified |
A ray of light is incident on an equilateral glass prism placed on a horizontal table as shown. For minimum deviation, a true statement is:


| 1. | \(PQ\) is horizontal |
| 2. | \(QR\) is horizontal |
| 3. | \(RS\) is horizontal |
| 4. | Either \(PQ\) or \(RS\) is horizontal |
| 1. | \(\frac{\sqrt{3}}{2} \) | 2. | \(1.5 \) |
| 3. | \(1.732 \) | 4. | \( 2\) |
A thin rod of length \(\frac{f}{3}\) lies along the axis of a concave mirror of focal length \(f\). One end of its magnified, real image touches an end of the rod. The length of the image is:
1. \(f\)
2. \(\frac{f}{2}\)
3. \(2f\)
4. \(\frac{f}{4}\)
A thin equiconvex lens of power \(P\) is cut into three parts \(A,B,\) and \(C\) as shown in the figure. If \(P_1,P_2\) and \(P_3\) are powers of the three parts respectively, then:
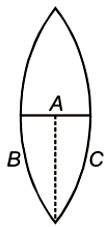

| 1. | \(P_1=P_2=P_3\) | 2. | \(P_1>P_2=P_3\) |
| 3. | \(P_1<P_2=P_3\) | 4. | \(P_2=P_3=2P_1\) |
A point source of light \(B\) is placed at a distance \(L\) in front of the centre of a mirror of width \(d\) hung vertically on a wall. A man \((A)\) walks in front of the mirror along a line parallel to the mirror at a distance \(2L\) from it as shown. The greatest distance over which he can see the image of the light source in the mirror is:

1. \(\frac{d}{2}\)
2. \(d\)
3. \(2d\)
4. \(3d\)
| 1. | \(32.75\) | 2. | \(327.5\) |
| 3. | \(0.3275\) | 4. | None of the above |


