Q. No.A disc is placed on the surface of a pond which has a refractive index of \(\frac{5}{3}.\) A source of light is placed \(4\) m below the surface of the liquid. Find The minimum radius of a disc so that light does not come out from it.
1. \(\infty\)
2. \(3~\text{m}\)
3. \(6~\text{m}\)
4. \(4~\text{m}\)
1. \(\infty\)
2. \(3~\text{m}\)
3. \(6~\text{m}\)
4. \(4~\text{m}\)
A ray of light travelling in the air has wavelength \(\lambda\), frequency \(n\), velocity \(v\), and intensity \(I\). If this ray enters into water then these parameters are \(\lambda', n', v'\) and \(I'\) respectively. Which relation is correct?
1. \(\lambda = \lambda'\)
2. \(n=n'\)
3. \(v=v'\)
4. \(I=I'\)
Optical fibre is based on:
1. Total internal reflection
2. Less scattering
3. Refraction
4. Less absorption coefficient
| 1. | become zero. |
| 2. | become infinite. |
| 3. | become small, but non-zero. |
| 4. | remain unchanged. |
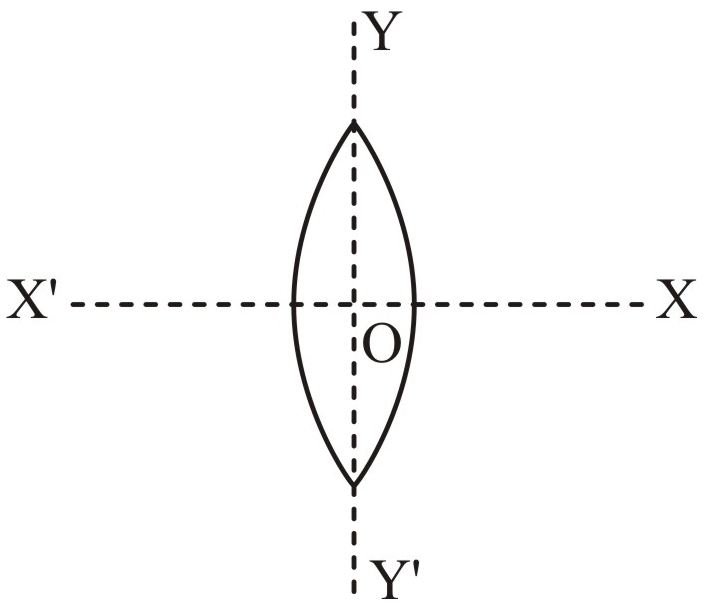
Choose the correct statement from the following:
| 1. | \(f' = f,f'' =2f\) | 2. | \(f' = 2f, f''=f\) |
| 3. | \(f' =f, f''=f\) | 4. | \(f'=2f, f''=2f\) |
In a compound microscope, the magnification is \(95\), the distance of the object from the objective lens is \(\frac{1}{3.8}~\text{cm}\) and the focal length of the objective is \(\frac{1}{4}~\text{cm}\). What is the magnification of the eyepiece when the final image is formed at the least distance of distinct vision?
| 1. | \(5\) | 2. | \(10\) |
| 3. | \(100\) | 4. | none of the above |
| 1. | Only \(\frac{d}{4}\) |
| 2. | Only \(\frac{d}{2}\) |
| 3. | More than \(\frac{d}{4}\) but less than \(\frac{d}{2}\) |
| 4. | Less than or equal to \(\frac{d}{4}\) |
If refractive index of a prism is \(\mathrm{cot(A/2)}\), then the minimum angle of deviation is:
1. \(180^{\circ}-A\)
2. \(180^{\circ}-2A\)
3. \(90^{\circ}-A\)
4. \((A/2)\)
For the given incident ray as shown in the figure, in the condition of the total internal reflection of this ray, the minimum refractive index of the prism will be:
| 1. | \(\dfrac{\sqrt{3} + 1}{2}\) | 2. | \(\dfrac{\sqrt{2} + 1}{2}\) |
| 3. | \(\sqrt{\dfrac{3}{2}}\) | 4. | \(\sqrt{\dfrac{7}{6}}\) |
The refractive index of the material of a prism is and its refracting angle is \(30^{\circ}\). One of the refracting surfaces of the prism is made a mirror inwards. A beam of monochromatic light entering the prism from the other face will retrace its path after reflection from the mirrored surface if its angle of incidence on the prism is:
| 1. | \(60^{\circ}\) | 2. | \(0^{\circ}\) |
| 3. | \(30^{\circ}\) | 4. | \(45^{\circ}\) |
© 2024 GoodEd Technologies Pvt. Ltd.