Q. No.An ideal resistance \(R,\) ideal inductance \(L,\) ideal capacitance \(C,\) and AC voltmeters \(V_1, V_2, V_3~\text{and}~V_4 \) are connected to an AC source as shown. At resonance:
1.
reading in \(V_3\) = reading in \(V_1\)
2.
reading in \(V_1\) = reading in \(V_2\)
3.
reading in \(V_2\) = reading in \(V_4\)
4.
reading in \(V_2\) = reading in \(V_3\)
A transistor-oscillator using a resonant circuit with an inductance \(L\) (of negligible resistance) and a capacitance \(C\) has a frequency \(f\). If \(L\) is doubled and \(C\) is changed to \(4C\), the frequency will be:
1. \(\frac{f}{4}\)
2. \(8f\)
3. \(\frac{f}{2\sqrt{2}}\)
4. \(\frac{f}{2}\)
| 1. | \(50\) V | 2. | \(50 \sqrt{2} ~\text{V}\) |
| 3. | \(100\) V | 4. | \(0\) V |
An AC voltage source is connected to a series \(LCR\) circuit. When \(L\) is removed from the circuit, the phase difference between current and voltage is \(\dfrac{\pi}{3}\). If \(C\) is instead removed from the circuit, the phase difference is again \(\dfrac{\pi}{3}\) between current and voltage. The power factor of the circuit is:
1. \(0.5\)
2. \(1.0\)
3. \(-1.0\)
4. zero
1. \(200~\text W\)
2. \(400~\text W\)
3. \(300~\text W\)
4. zero
A direct current of \(5~ A\) is superimposed on an alternating current \(I=10sin ~\omega t\) flowing through a wire. The effective value of the resulting current will be:
| 1. | \(15/2~A\) | 2. | \(5 \sqrt{3}~A\) |
| 3. | \(5 \sqrt{5}~A\) | 4. | \(15~A\) |
If \(q\) is the capacitor's charge and \(i\) is the current at time \(t\), the voltage \(V\) will be:
| 1. | \(L \frac{di}{dt}+{iR}-\frac{q}{C}=V\) |
| 2. | \(L \frac{di}{dt}-{iR}+\frac{q}{C}=V\) |
| 3. | \(L \frac{di}{dt}+{iR}+\frac{q}{C}=V\) |
| 4. | \(L\frac{di}{dt}-{iR}-\frac{q}{C}=V\) |
An AC ammeter is used to measure the current in a circuit. When a given direct current passes through the circuit, the AC ammeter reads \(6~\text A.\) When another alternating current passes through the circuit, the AC ammeter reads \(8~\text A.\) Then the reading of this ammeter if DC and AC flow through the circuit simultaneously is:
1. \(10 \sqrt{2}~\text A\)
2. \(14~\text A\)
3. \(10~\text A\)
4. \(15~\text A\)
The AC source in the circuit shown in the figure produces a voltage \(V = 20\cos(2000t)\) volts. Neglecting source resistance, the voltmeter and ammeter readings will be (approximately):
| 1. | \(4~\text{V}, 2.0~\text{A}\) | 2. | \(0~\text{V}, 2~\text{A}\) |
| 3. | \(5.6~\text{V}, 1.4~\text{A}\) | 4. | \(8~\text{V}, 2.0~\text{A}\) |
In the circuit shown, the AC source has a voltage
\(V= 20\cos(\omega t)\) volts with \(\omega = 2000\) rad/s. The amplitude of the current will be nearest to:
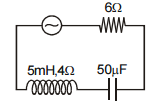
1. \(2\) A
2. \(3.3\) A
3. \(\frac{2}{\sqrt{5}}\) A
4. \(\sqrt{5}\) A
© 2025 GoodEd Technologies Pvt. Ltd.