- 1(current)
Q. No.The variation of induced emf (E) with time (t) in a coil if a short bar magnet is moved along its axis with a constant velocity is best represented as:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
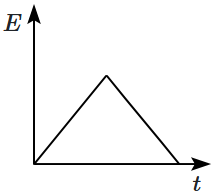| Assertion (A): | Lenz's law is in accordance with the conservation of energy. |
| Reason (R): | The amount of mechanical energy lost against the induced emf or current is equal to the electrical energy reappearing in the circuit. |
In the light of the above statements choose the correct answer from the options given below:
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | Both (A) and (R) are false. |
A rectangular loop and a circular loop are moving out of a uniform magnetic field region (as shown in the figure) to a field-free region with a constant velocity \(v.\) In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops:
1. only in the case of the rectangular loop
2. only in the case of the circular loop
3. in both cases
4. none of these
The current \(i\) in a coil varies with time as shown in the figure. The variation of induced emf with time would be:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| Assertion (A): | Faraday's law of electromagnetic induction is not consistent with the law of conservation of energy. |
| Reason (R): | Lenz's law is consistent with energy conservation. |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| Assertion (A): | Faraday's law of electromagnetic induction is a consequence of Biot-Savart's law. |
| Reason (R): | Currents cause magnetic fields and interact with magnetic flux. |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.