A battery of internal resistance \(r\), when connected across \(2~\Omega\) resistor supplies a current of \(4~\text{A}\). When the battery is connected across a \(5~\Omega\) resistor, it supplies a current of \(2~\text{A}\). The value of \(r\) is:
1.
\(2~\Omega\)
2
\(1~\Omega\)
3.
\(0.5~\Omega\)
4.
zero
In the circuit shown in the figure below, the current supplied by the battery is:

1. \(2~\text A\)
2. \(1~\text A\)
3. \(0.5~\text A\)
4. \(0.4~\text A\)
The figure below shows a network of currents. The current \(i\) will be:

1. \(3~\text{A}\)
2. \(13~\text{A}\)
3. \(23~\text{A}\)
4. \(-3~\text{A}\)
Power consumed in the given circuit is \(P_1.\) On interchanging the position of \(3~\Omega\) and \(12~\Omega\) resistances, the new power consumption is \(P_2.\) The ratio of \(\dfrac{P_2}{P_1}\) is:
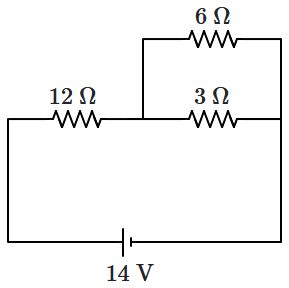
| 1. | \(2\) | 2. | \(\dfrac 12\) |
| 3. | \(\dfrac 35\) | 4. | \(\dfrac 25\) |
| 1. | \(10^{\circ}\text{C}\) | 2. | \(5^{\circ}\text{C}\) |
| 3. | \(20^{\circ}\text{C}\) | 4. | \(15^{\circ}\text{C}\) |
What is the reading of the voltmeter of resistance \(1200~\Omega\) connected in the following circuit diagram?
| 1. | \(2.5\) V | 2. | \(5.0\) V |
| 3. | \(7.5\) V | 4. | \(40\) V |
The dependence of resistivity \((\rho)\) on the temperature \((T)\) of a semiconductor is, roughly, represented by:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Current through the \(2~\Omega\) resistance in the electrical network shown is:

| 1. | zero | 2. | \(1~\text A\) |
| 3. | \(3~\text A\) | 4. | \(5~\text A\) |
Two batteries, one of emf \(18~\text{V}\) and internal resistance \(2~\Omega\) and the other of emf \(12~\text V\) and internal resistance \(1~\Omega,\) are connected as shown. Reading of the voltmeter is:
(if a voltmeter is ideal)

1. \(14~\text V\)
2. \(15~\text V\)
3. \(18~\text V\)
4. \(30~\text V\)
The metre bridge shown is in a balanced position with \(\frac{P}{Q} = \frac{l_1}{l_2}\). If we now interchange the position of the galvanometer and the cell, will the bridge work? If yes, what will be the balanced condition?
| 1. | Yes, \(\frac{P}{Q}=\frac{l_1-l_2}{l_1+l_2}\) | 2. | No, no null point |
| 3. | Yes, \(\frac{P}{Q}= \frac{l_2}{l_1}\) | 4. | Yes, \(\frac{P}{Q}= \frac{l_1}{l_2}\) |








