- 1(current)
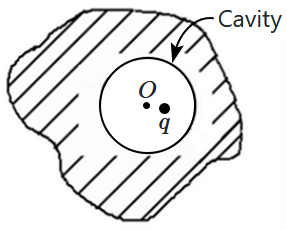
Q. No.A point charge \(q\) is placed within a spherical cavity inside a metallic conductor, slightly off-centre. The charge \(q\) induces a charge distribution on the inner surface of the cavity. The net force on \(q\) due to the induced charges is:
| 1. | zero |
| 2. | towards the centre |
| 3. | away from the centre |
| 4. | either towards or away from the centre depending on the sign of \(q\) |
Subtopic: Â Gauss's Law |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Given below are two statements:
| Statement I: | Gauss's law for electric fields is a consequence of the conservation of energy. |
| Statement II: | Coulomb's law for electric charges leads to a conservative electric field. |
| 1. | Statement I is incorrect and Statement II is correct. |
| 2. | Both Statement I and Statement II are correct. |
| 3. | Both Statement I and Statement II are incorrect. |
| 4. | Statement I is correct and Statement II is incorrect. |
Subtopic: Â Gauss's Law |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
An electric dipole of dipole moment \(p\) is placed at the centre of a spherical surface of radius \(R.\) The net flux of the electric field of the dipole through the hemisphere, where it is positive, is proportional to:
1. \(R\)
2. \(R^{-3}\)
3. \(R^{-2}\)
4. \(R^{-1}\)
1. \(R\)
2. \(R^{-3}\)
3. \(R^{-2}\)
4. \(R^{-1}\)
Subtopic: Â Gauss's Law |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
A solid sphere carrying a uniformly distributed charge \(q\) within its volume rotates about a diameter \((d = 2r ).\) So that the speed on its equator is \(v.\) The electric field at the outer surface of the sphere is:
1. \(\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{q}{r^{2}}\)
2. \(\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{q}{3 r^{2}}\)
3. \(\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{q}{2 r^{2}}\)
4. \(\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{2q}{r^{2}}\)
Subtopic: Â Gauss's Law |
From NCERT
Please attempt this question first.
Hints
Links
Please attempt this question first.
A point charge '\(q\)' is placed at the centre of a spherical cavity at the centre of a conducting sphere. The sphere is initially uncharged. The radius of the cavity is '\(a\)' and that of the sphere is '\(2a\)'. Let the charge on the outer surface of the sphere be \(Q\).
Then,
Then,
| 1. | \(q,Q\) are of the same sign and \(|q|=|Q|\) |
| 2. | \(q,Q\) are of opposite signs and \(|q|=|Q|\) |
| 3. | \(q,Q\) are of the same sign and \(|q|<|Q|\) |
| 4. | \(q,Q\) are of opposite signs and \(|q|>|Q|\) |
Subtopic: Â Gauss's Law |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
A point charge \(q\) is placed at the centre of the flat surface of a semi-infinite cylinder of radius \(r.\) The flux of its electric field through the curved surface of the cylinder is:
| 1. | \(\dfrac{q}{\varepsilon_0}\) | 2. | \(\dfrac{q}{2\varepsilon_0}\) |
| 3. | \(\dfrac{2q}{\varepsilon_0}\) | 4. | \(0\) |
Subtopic: Â Gauss's Law |
 54%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
A point charge \(q\) (positive) is placed just below the centre \(O\) of the top face of a cylinder of height \(h,\) and radius \(r:\) \(h\gg r.\) The flux of the electric field of the charge \(q\) through the top face is \(\phi_t,\) through the bottom face is \(\phi_b\) and through the curved face of the cylinder is \(\phi_c.\) Then, one can conclude,
1. \(\phi_t<\phi_c<\phi_b\)
2. \(\phi_t<\phi_b<\phi_c\)
3. \(\phi_t>\phi_c>\phi_b\)
4. \(\phi_t>\phi_b>\phi_c\)
1. \(\phi_t<\phi_c<\phi_b\)
2. \(\phi_t<\phi_b<\phi_c\)
3. \(\phi_t>\phi_c>\phi_b\)
4. \(\phi_t>\phi_b>\phi_c\)
Subtopic: Â Gauss's Law |
 56%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Two identical point charges, \(q\) each, are placed at the opposite ends of a long diagonal of a cube. The flux of the electric field, due to these charges, out of the cube, is:
| 1. | \(\dfrac{q}{\varepsilon_0}\) | 2. | \(\dfrac{q}{2\varepsilon_0}\) |
| 3. | \(\dfrac{q}{4\varepsilon_0}\) | 4. | \(\dfrac{q}{8\varepsilon_0}\) |
Subtopic: Â Gauss's Law |
 59%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.