The translational kinetic energy of \(n\) moles of a diatomic gas at absolute temperature \(T\) is given by:
1. \(\frac{5}{2}nRT\)
2. \(\frac{3}{2}nRT\)
3. \(5nRT\)
4. \(\frac{7}{2}nRT\)

If the pressure of a gas is doubled, then the average kinetic energy per unit volume of the gas will be:

If at a pressure of \(10^6\) dyne/cm², one gram of nitrogen occupies \(2\times10^4\) c.c. volume, then the average energy of a nitrogen molecule in erg is:

Two isotherms are drawn at temperatures ${\mathrm{T}}_1$ $\mathrm{and}$ ${\mathrm{T}}_2$ as shown. The ratio of mean speed  at ${\mathrm{T}}_1$ $\mathrm{and}$ ${\mathrm{T}}_2$ is:
  

The translational kinetic energy of oxygen molecules at room temperature is \(60~\text J.\) Their rotational kinetic energy will be?
1. \(40~\text J\)
2. \(60~\text J\)
3. \(50~\text J\)
4. \(20~\text J\)

When the gas in an open container is heated, the mean free path:
1. Increases
2. Decreases
3. Remains the same
4. Any of the above depending on the molar mass

The change in the internal energy of an ideal gas does not depend on?

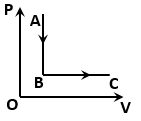
The figure shows a process for a gas in which pressure (P) and volume (V) of the gas change. If $C_1$ and $C_2$ are the molar heat capacities of the gas during the processes AB and BC respectively, then:

1. $C_1=C_2$

2. $C_1>C_2$

3. $C_1<C_2$

4. $C_1\le C_2$

In the PV graph shown below for an ideal diatomic gas, the change in the internal energy is:
     

1. $\frac{3}{2}\mathrm{P}({\mathrm{V}}_2-{\mathrm{V}}_1)$

2. $\frac{5}{2}\mathrm{P}({\mathrm{V}}_2-{\mathrm{V}}_1)$

3. $\frac{3}{2}\mathrm{P}({\mathrm{V}}_1-{\mathrm{V}}_2)$

4. $\frac{7}{2}\mathrm{P}({\mathrm{V}}_1-{\mathrm{V}}_2)$

How does the pressure of an ideal gas change during the process shown in the diagram?