From a solid sphere of mass \(M\) and radius \(R\) a cube of maximum possible volume is cut. The moment of inertia of a cube about an axis passing through its center and perpendicular to one of its faces is:
1. \( \frac{{MR}^2}{32 \sqrt{2 \pi}} \)
2. \( \frac{{MR}^2}{16 \sqrt{2} \pi} \)
3. \( \frac{4 {MR}^2}{9 \sqrt{3} \pi} \)
4. \( \frac{4{MR}^2}{3 \sqrt{3} \pi}\)
1. \({I}>\dfrac{{ma}^2}{12}\)
2. \({I}=\dfrac{{ma}^2}{12}\)
3. \(\dfrac{{ma}^2}{24}<{I}<\dfrac{{ma}^2}{12}\)
4. \({I}=\dfrac{{ma}^2}{24}\)

1. \(\frac{31}{32}I_0\)
2. \(\frac{3}{4}I_0\)
3. \(\frac{7}{8}{I}_0\)
4. \(\frac{15}{16}{I}_0\)

| 1. | \(\dfrac{219~{MR}^2}{256}\) | 2. | \(\dfrac{197{MR}^2}{256}\) |
| 3. | \(\dfrac{19{MR}^2}{512}\) | 4. | \(\dfrac{237{MR}^2}{512}\) |
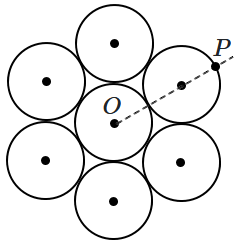
Seven identical circular planar disks, each of mass \(M\) and radius \(R\) are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point \(P\) is:
1. \(\frac{19}{2}{MR}^2\)
2. \(\frac{55}{2}{MR}^2\)
3. \(\frac{73}{2}{MR}^2\)
4. \(\frac{181}{2}{MR}^2\)
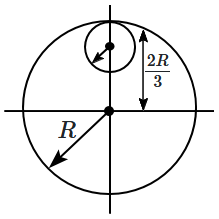
From a uniform circular disc of radius \(R\) and mass \(9M\), a small disc of radius \(\frac{R}{3}\) is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of the disc is:
1. \( 4{MR}^2 \)
2. \( \frac{40}{9}{MR}^2 \)
3. \( 10{MR}^2 \)
4. \( \frac{37}{9}{MR}^2\)

1. \(1 : 4\)
2. \(1 : 5\)
3. \(1 : 3\)
4. \(1 : 2\)
A thin circular plate of mass \(M\) and radius \(R\) has its density varying as \(\rho(r)=\rho_0 r\) with \(\rho_0\) as constant and \(r\) is the distance from its center. The moment of inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is \(I=\alpha MR^2\). The value of the coefficient \(\alpha\) is:
1. \(\frac{3}{2}\)
2. \(\frac{1}{2}\)
3. \(\frac{8}{5}\)
4. \(\frac{3}{5}\)
A thin disc of mass \(M\) and radius \(R\) has mass per unit area \(\sigma(r)=kr^2\) where \(r\) is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is:
1. \(\frac{2MR^2}{3}\)
2. \(\frac{MR^2}{6}\)
3. \(\frac{MR^2}{3}\)
4. \(\frac{MR^2}{2}\)
A solid sphere of mass \(M\) and radius \(R\) is divided into two unequal parts. The first part has a mass of \(\frac{7M}{8}\) and is converted into a uniform disc of radius \(2R\). The second part is converted into a uniform solid sphere. Let \(I_1\) be the moment of inertia of the disc about its axis and \(I_2\) be the moment of inertia of the new sphere about its axis. The ratio \(\frac{I_1}{I_2}\) is given by:
1. \(65\)
2. \(140\)
3. \(185\)
4. \(285\)