Five particles of mass \(2\) kg each are attached to the circumference of a circular disc of a radius of \(0.1\) m and negligible mass. The moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane will be:
1. \(1\) kg-m²
2. \(0.1\) kg-m²
3. \(2\) kg-m²
4. \(0.2\) kg-m²

The moment of inertia of a uniform circular disc of radius '\(R\)' and mass '\(M\)' about an axis touching the disc at its diameter and normal to the disc will be:
1. \(\frac{3}{2} M R^{2}\)
2. \(\frac{1}{2} M R^{2}\)
3. \(M R^{2}\)
4. \(\frac{2}{5} M R^{2}\)${\mathrm{}}^{}$

The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
 
1. B                   
2. C
3. D                   
4. A

The moment of inertia of a thin uniform circular disc about one of its diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its center will be:

1. $\sqrt{2}I$

2. 2 l

3. $\frac{I}{2}$

4. $\frac{I}{\sqrt{2}}$

The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring will be:
1. \(2:1\)
2. $\sqrt{5}$ : $\sqrt{6}$
3. \(2:3\)
4. \(1:\) $\sqrt{2}$

In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:

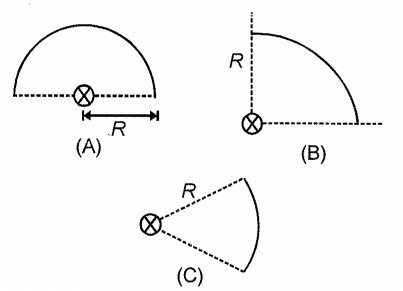
1.  $I_A$ $>$ $I_B$ $>$ $$ $I_C$

2.  $I_A$ $=$ $I_B$ $=$ $I_C$

3.  $I_A$ $<$ $I_B$ $<$ $I_C$

4.  $I_A$ $<$ $I_C$ $<$ $I_B$

Three-point masses each of mass \(m,\) are placed at the vertices of an equilateral triangle of side \(a.\) The moment of inertia of the system through a mass \(m\) at \(O\) and lying in the plane of \(COD\) and perpendicular to \(OA\) is: