A force \(\vec{F}=\alpha\hat i+3\hat j+6\hat k\) is acting at a point \(\vec{r}=2\hat i-6\hat j-12\hat k.\) The value of \(\alpha\)
for which angular momentum is conserved about the origin is:
1. \(-1\)
2. \(2\)
3. zero
4. \(1\)
1. \(-1\)
2. \(2\)
3. zero
4. \(1\)
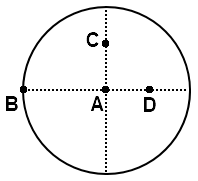
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
1. B
2. C
3. D
4. A
Three masses are placed on the x-axis: \(300\) g at the origin, \(500\) g at \(x =40\) cm, and \(400\) g at \(x=70\) cm. The distance of the center of mass from the origin is:
1. \(40\) cm
2. \(45\) cm
3. \(50\) cm
4. \(30\) cm
Two rotating bodies \(A\) and \(B\) of masses \(m\) and \(2m\) with moments of inertia \(I_A\) and \(I_B\) \((I_B>I_A)\) have equal kinetic energy of rotation. If \(L_A\) and \(L_B\) be their angular momenta respectively, then:
1. \(L_{A} = \frac{L_{B}}{2}\)
2. \(L_{A} = 2 L_{B}\)
3. \(L_{B} > L_{A}\)
4. \(L_{A} > L_{B}\)
1. \(1\)
2. \(2\)
3. \(3\)
4. \(4\)
| 1. | \(\dfrac{m_1m_2}{m_1+m_2}l^2\) | 2. | \(\dfrac{m_1+m_2}{m_1m_2}l^2\) |
| 3. | \((m_1+m_2)l^2\) | 4. | \(\sqrt{(m_1m_2)}l^2\) |
| 1. | \(wx \over d\) | 2. | \(wd \over x\) |
| 3. | \(w(d-x) \over x\) | 4. | \(w(d-x) \over d\) |
A solid cylinder of mass \(50~\text{kg}\) and radius \(0.5~\text{m}\) is free to rotate about the horizontal axis. A massless string is wound around the cylinder with one end attached to it and the other end hanging freely. The tension in the string required to produce an angular acceleration of \(2~\text{rev/s}^2\) will be:
1. \(25~\text N\)
2. \(50~\text N\)
3. \(78.5~\text N\)
4. \(157~\text N\)
A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m are attached gently to the opposite ends of the diameter of the ring, the ring will then rotate with an angular velocity:
| 1. | \(\frac{\omega(M-2 m)}{M+2 m} \) | 2. | \(\frac{\omega M}{M+2 m} \) |
| 3. | \(\frac{\omega(M+2 m)}{M} \) | 4. | \(\frac{\omega M}{M+m}\) |
Which of the following will not be affected if the radius of the sphere is increased while keeping mass constant?
| 1. | Moment of inertia | 2. | Angular momentum |
| 3. | Angular velocity | 4. | Rotational kinetic energy |