A wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first \(2\) s, it rotates through an angle \(\theta_1\). In the next \(2\) s, it rotates through an additional angle \(\theta_2\). The ratio of \(\frac{\theta_2}{\theta_1}\) is:
1. \(1\)
2. \(2\)
3. \(3\)
4. \(4\)
Two rotating bodies \(A\) and \(B\) of masses \(m\) and \(2m\) with moments of inertia \(I_A\) and \(I_B\) \((I_B>I_A)\) have equal kinetic energy of rotation. If \(L_A\) and \(L_B\) be their angular momenta respectively, then:
1. \(L_{A} = \frac{L_{B}}{2}\)
2. \(L_{A} = 2 L_{B}\)
3. \(L_{B} > L_{A}\)
4. \(L_{A} > L_{B}\)
A force \(\vec{F}=\alpha\hat i+3\hat j+6\hat k\) is acting at a point \(\vec{r}=2\hat i-6\hat j-12\hat k.\) The value of \(\alpha\)
for which angular momentum is conserved about the origin is:
1. \(-1\)
2. \(2\)
3. zero
4. \(1\)
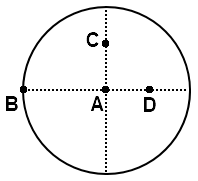
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
1. B
2. C
3. D
4. A
Three masses are placed on the x-axis: \(300\) g at the origin, \(500\) g at \(x =40\) cm, and \(400\) g at \(x=70\) cm. The distance of the center of mass from the origin is:
1. \(40\) cm
2. \(45\) cm
3. \(50\) cm
4. \(30\) cm
Which of the following will not be affected if the radius of the sphere is increased while keeping mass constant?
| 1. | Moment of inertia | 2. | Angular momentum |
| 3. | Angular velocity | 4. | Rotational kinetic energy |
Four particles of mass \(m_1 = 2m\), \(m_2=4m\), \(m_3 =m \), and \(m_4\) are placed at the four corners of a square. What should be the value of \(m_4\) so that the centre of mass of all the four particles is exactly at the centre of the square?

1. \(2m\)
2. \(8m\)
3. \(6m\)
4. None of these
A rigid body rotates about a fixed axis with a variable angular velocity equal to \(\alpha -\beta t\), at the time \(t\), where \(\alpha , \beta\) are constants. The angle through which it rotates before it stops is:
| 1. | \(\frac{\alpha^{2}}{2 \beta}\) | 2. | \(\frac{\alpha^{2} -\beta^{2}}{2 \alpha}\) |
| 3. | \(\frac{\alpha^{2} - \beta^{2}}{2 \beta}\) | 4. | \(\frac{\left(\alpha-\beta\right) \alpha}{2}\) |
The position of a particle is given by \(\vec r = \hat i+2\hat j-\hat k\) and momentum \(\vec P = (3 \hat i + 4\hat j - 2\hat k)\). The angular momentum is perpendicular to:
| 1. | X-axis |
| 2. | Y-axis |
| 3. | Z-axis |
| 4. | Line at equal angles to all the three axes |
The centre of the mass of \(3\) particles, \(10~\text{kg},\) \(20~\text{kg},\) and \(30~\text{kg},\) is at \((0,0,0).\) Where should a particle with a mass of \(40~\text{kg}\) be placed so that its combined centre of mass is \((3,3,3)?\)
1. \((0,0,0)\)
2. \((7.5, 7.5, 7.5)\)
3. \((1,2,3)\)
4. \((4,4,4)\)