A particle is moving such that the potential energy U varies with position in metre as U (x) = ( - 2x + 50) J. The particle will be in equilibrium at:
1. x = 25 cm
2. x = 2.5 cm
3. x = 25 m
4. x = 2.5 m
1. x = 25 cm
2. x = 2.5 cm
3. x = 25 m
4. x = 2.5 m
Select the incorrect statement about potential energy:
| 1. | A change in potential energy is equal to work done against the internal conservative force.
|
| 2. | A change in potential energy is independent of the reference point.
|
| 3. | A change in potential energy depends on the reference frame.
|
| 4. | The potential energy at a point is not unique. |
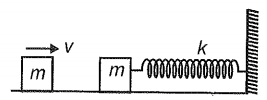
1. \(v\sqrt{\dfrac{m}{k}}\)
2. \(v\sqrt{\dfrac{2m}{k}}\)
3. \(m\sqrt{\dfrac{v}{2k}}\)
4. \(v\sqrt{\dfrac{m}{2k}}\)
The figure shows the potential energy function U of a system in which a particle is in one-dimensional motion. In which region is the magnitude of the force on the particle greatest? (x: position)
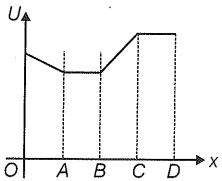
| 1. | OA | 2. | CD |
| 3. | AB | 4. | BC |
Which of the following is not a unit of energy?
1. watt-hour
2. joule
3. eV
4. N/m
Four situations are shown in the following options. In each situation, planes are equally rough and the block begins with the same speed and slides until the kinetic frictional force has stopped it. In which of the following cases increase in thermal energy due to sliding is least?
| 1. | 2. |  |
|
| 3. | 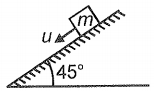 |
4. | 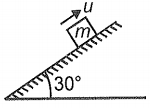 |
A block of mass m is placed in an elevator moving down with an acceleration . The work done by the normal reaction on the block as the elevator moves down through a height h is:
1.
2.
3.
4.
The potential energy of a particle varies with distance \(r\) as shown in the graph. The force acting on the particle is equal to zero at:

1. \(P\)
2. \(S\)
3. both \(Q\) and \(R\)
4. both \(P\) and \(S\)
1. \(\dfrac{2 um}{m}\)
2. \(\dfrac{2 um}{M}\)
3. \(\dfrac{2 u}{1 + {m \over M}}\)
4. \(\dfrac{2 u}{1 + {M \over m}}\)
Work done by frictional force during the walking of a man is:
1. positive
2. negative
3. zero
4. maybe positive or negative






