A point particle of mass \(m\), moves along the uniformly rough track \(PQR\) as shown in the figure. The coefficient of friction, between the particle and the rough track equals \(\mu\). The particle is released, from rest, from the point \(P\) and it comes to rest at a point \(R\). The energies, lost by the ball, over the parts, \(PQ\) and \(QR\), of the track, are equal to each other, and no energy is lost when the particle changes direction from \(PQ\) to \(QR\).
The values of the coefficient of friction \(\mu\) and the distance \(x~(=QR)\), are, respectively close to:

             
1. \(0.2~\text{and}~6.5~\text{m}\)
2. \(0.2~\text{and}~3.5~\text{m}\)
3. \(0.29~\text{and}~3.5~\text{m}\)
4. \(0.29~\text{and}~6.5~\text{m}\)

A time dependent force \(F = 6t \) acts on a particle of mass \(1~\text{kg}.\) If the particle starts from rest, the work done by the force during the first \(1~\text s\) will be:
1. \(4.5~\text{J}\)
2. \(22~\text{J}\)
3. \(9~\text{J}\)
4. \(18~\text{J}\)

A particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled \(3~\text{m}\) is:

1. \(2.5~\text{J}\)
2. \(6.5~\text{J}\)
3. \(4~\text{J}\)
4. \(5~\text{J}\)

A uniform cable of mass \(M\) and length \(L\) is placed on a horizontal surface such that its \(\left ( \dfrac{1}{n} \right )^\text{th}\) part is hanging below the edge of the surface. To lift the hanging part of the cable up to the surface, the work done should be:

A bullet of mass \(20~\text{g}\) has an initial speed of \(1~\text{ms}^{-1}\),  just before it starts penetrating a mud wall of thickness \(20~\text{cm}\). If the wall offers a mean resistance of \(2.5\times10^{-2}~\text{N}\), the speed of the bullet after emerging from the other side of the wall is close to:
1. \(0.3~\text{ms}^{-1}\)
2. \(0.1~\text{ms}^{-1}\)
3. \(0.7~\text{ms}^{-1}\)
4. \(0.4~\text{ms}^{-1}\)

A small block starts slipping down from a point \(B\) on an inclined plane \(AB,\) which is making an angle \(\theta\) with the horizontal. Section \(BC\) is smooth and the remaining section \(CA\) is rough with a coefficient of friction \(\mu\). It is found that the block comes to rest as it reaches the bottom (point \(A\)) of the inclined plane. If \(BC = 2AC,\) the coefficient of friction is given by \(\mu=k\tan\theta\). The value of \(k\) is:
           
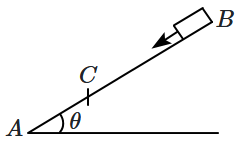
1. \(4\)
2. \(3\)
3. \(2\)
4. \(1\)

A cricket ball of mass \(0.15~\text{kg}\) is thrown vertically up by a bowling machine so that it rises to a maximum height of \(20~\text{m}\) after leaving the machine. If the part pushing the ball applies a constant force \(F\) on the ball and moves horizontally a distance of \(0.2~\text{m}\) while launching the ball, the value of \(F\) (in N) is: (\(g = 10\) m/s²)
1. \(50\)
2. \(100\)
3. \(150\)
4. \(200\)