- 1(current)
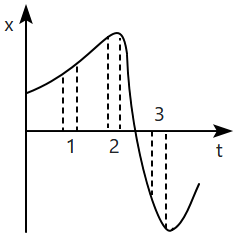
Q. No.The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:
| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |
Subtopic: Average Speed & Average Velocity |
90%
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
If a body travels some distance in a given time interval, then for that time interval, its:
| 1. | Average speed ≥ |Average velocity| |
| 2. | |Average velocity| ≥ Average speed |
| 3. | Average speed < |Average velocity| |
| 4. | |Average velocity| must be equal to average speed. |
Subtopic: Average Speed & Average Velocity |
85%
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A car moves from \(X\) to \(Y\) with a uniform speed \(v_u\) and returns to \(X\) with a uniform speed \(v_d.\) The average speed for this round trip is:
| 1. | \(\dfrac{2 v_{d} v_{u}}{v_{d} + v_{u}}\) | 2. | \(\sqrt{v_{u} v_{d}}\) |
| 3. | \(\dfrac{v_{d} v_{u}}{v_{d} + v_{u}}\) | 4. | \(\dfrac{v_{u} + v_{d}}{2}\) |
Subtopic: Average Speed & Average Velocity |
83%
From NCERT
AIPMT - 2007
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.