A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:

| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |
A car moves with a speed of \(60\) km/h for \(1\) hour in the east direction and with the same speed for \(30\) min in the south direction. The displacement of the car from the initial position is:
| 1. | \(60\) km | 2. | \(30 \sqrt{2}\) km |
| 3. | \(30 \sqrt{5}\) km | 4. | \(60 \sqrt{2}\) km |
For the given acceleration \(\left ( a \right )\) versus time \(\left ( t \right )\) graph of a body, the body is initially at rest.
From the following, the velocity \(\left ( v \right )\) versus time \(\left ( t \right )\) graph will be:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle moves along a path \(ABCD\) as shown in the figure. The magnitude of the displacement of the particle from \(A\) to \(D\) is:
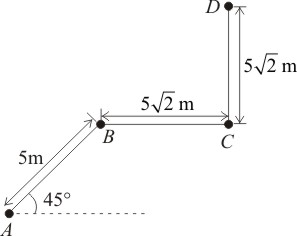
1. m
2. \(10\) m
3. m
4. \(15\) m
The displacement \(x\) of a particle varies with time \(t\) as \(x = ae^{-\alpha t}+ be^{\beta t}\), where \(a,\) \(b,\) \(\alpha,\) and \(\beta\) are positive constants. The velocity of the particle will:
| 1. | be independent of \(\alpha\) and \(\beta.\) |
| 2. | go on increasing with time. |
| 3. | drop to zero when \(\alpha=\beta.\) |
| 4. | go on decreasing with time. |
If a body travels some distance in a given time interval, then for that time interval, its:
| 1. | Average speed ≥ |Average velocity| |
| 2. | |Average velocity| ≥ Average speed |
| 3. | Average speed < |Average velocity| |
| 4. | |Average velocity| must be equal to average speed. |
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity \({v_0}\) and the braking capacity, or deceleration, \(-a\) that is caused by the braking. Expression for stopping distance of a vehicle in terms of \({v_0}\) and \(a\) is:
| 1. | \(\dfrac{{v_o}^2}{2a}\) | 2. | \(\dfrac{{v_o}}{2a}\) |
| 3. | \(\dfrac{{v_o}^2}{a}\) | 4. | \(\dfrac{2a}{{v_o}^2}\) |
The position of an object moving along the \(x\text-\)axis is given by, \(x=a+bt^2\), where \(a=8.5 ~\text m,\) \(b=2.5~\text{m/s}^2,\) and \(t\) is measured in seconds. Its velocity at \(t=2.0~\text s\) will be:
1. \(13~\text{m/s}\)
2. \(17~\text{m/s}\)
3. \(10~\text{m/s}\)
4. \(0~\text{m/s}\)
The figure shows the displacement-time graph of a particle moving on the x-axis. Then,
| 1. | the particle is continuously going in a positive x-direction. |
| 2. | the particle is at rest. |
| 3. | the velocity increases up to a time \(t_0\), and then becomes constant. |
| 4. | the particle moves at a constant velocity up to a time \(t_0\), and then stops. |








