For the given acceleration \(\left ( a \right )\) versus time \(\left ( t \right )\) graph of a body, the body is initially at rest.

From the following, the velocity \(\left ( v \right )\) versus time \(\left ( t \right )\) graph will be:
1.

2.

3.

4.


From the following, the velocity \(\left ( v \right )\) versus time \(\left ( t \right )\) graph will be:




A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
A particle moves along a path \(ABCD\) as shown in the figure. The magnitude of the displacement of the particle from \(A\) to \(D\) is:
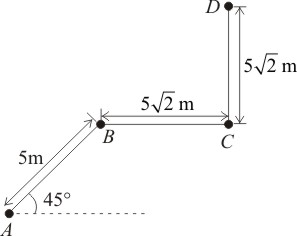
1. m
2. \(10\) m
3. m
4. \(15\) m
The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:

| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |
A car moves with a speed of \(60\) km/h for \(1\) hour in the east direction and with the same speed for \(30\) min in the south direction. The displacement of the car from the initial position is:
| 1. | \(60\) km | 2. | \(30 \sqrt{2}\) km |
| 3. | \(30 \sqrt{5}\) km | 4. | \(60 \sqrt{2}\) km |
The graph of displacement time is given below.
Its corresponding velocity-time graph will be:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle moving along the x-axis has acceleration \(f,\) at time \(t,\) given by, \(f=f_0\left ( 1-\frac{t}{T} \right ),\) where \(f_0\) and \(T\) are constants. The particle at \(t=0\) has zero velocity. In the time interval between \(t=0\) and the instant when \(f=0,\) the particle’s velocity \( \left ( v_x \right )\) is:
1. \(f_0T\)
2. \(\frac{1}{2}f_0T^{2}\)
3. \(f_0T^2\)
4. \(\frac{1}{2}f_0T\)
A car moves from \(X\) to \(Y\) with a uniform speed \(v_u\) and returns to \(X\) with a uniform speed \(v_d.\) The average speed for this round trip is:
| 1. | \(\dfrac{2 v_{d} v_{u}}{v_{d} + v_{u}}\) | 2. | \(\sqrt{v_{u} v_{d}}\) |
| 3. | \(\dfrac{v_{d} v_{u}}{v_{d} + v_{u}}\) | 4. | \(\dfrac{v_{u} + v_{d}}{2}\) |
The distance travelled by a particle starting from rest and moving with an acceleration \(\frac{4}{3}\) ms-2, in the third second is:
1. \(6\) m
2. \(4\) m
3. \(\frac{10}{3}\) m
4. \(\frac{19}{3}\) m
A particle moves a distance \(x\) in time \(t\) according to equation \(x=(t+5)^{-1}.\) The acceleration of the particle is proportional to:
1. (velocity)\(3/2\)
2. (distance)\(2\)
3. (distance)\(-2\)
4. (velocity)\(2/3\)







