A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:

| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |
| 1. | zero velocity. | 2. | zero acceleration. |
| 3. | non-zero velocity. | 4. | non-zero acceleration. |
When the velocity of a body is variable, then:
| 1. | its speed may be constant |
| 2. | its acceleration may be constant |
| 3. | its average acceleration may be constant |
| 4. | all of the above |
A body is projected vertically in the upward direction from the surface of the earth. If the upward direction is taken as positive, then the acceleration of the body during its upward and downward journey is:
| 1. | Positive, negative | 2. | Negative, negative |
| 3. | Positive, positive | 4. | Negative, positive |
Which one of the following displacement-time graph represents two moving objects \(P\) and \(Q\) with zero relative velocity?
| 1. | 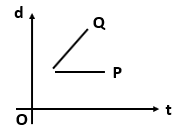 |
2. | 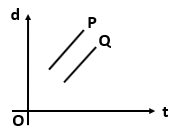 |
| 3. | 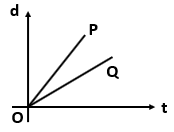 |
4. | 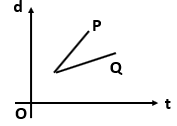 |
A particle starts from rest (with constant acceleration) and acquires velocity \(20\) m/s in \(5\) s. The distance travelled by the particle in the next \(2\) s will be:
| 1. | \(50\) m | 2. | \(48\) m |
| 3. | \(100\) m | 4. | \(150\) m |
A body is thrown upwards and reaches its maximum height. At that position:
| 1. | its velocity is zero and its acceleration is also zero. |
| 2. | its velocity is zero but its acceleration is maximum. |
| 3. | its acceleration is minimum. |
| 4. | its velocity is zero and its acceleration is the acceleration due to gravity. |
A ball is thrown vertically downwards with a velocity of \(20\) m/s from the top of a tower. It hits the ground after some time with the velocity of \(80\) m/s . The height of the tower is: (assuming \(g = 10~\text{m/s}^2)\)
| 1. | \(340\) m | 2. | \(320\) m |
| 3. | \(300\) m | 4. | \(360\) m |
If in one-dimensional motion, instantaneous speed \(v\) satisfies \(0\leq v<v_0,\) then:
| 1. | the displacement in time \(T\) must always take non-negative values. |
| 2. | the displacement \(x\) in time \(T\) satisfies \(-{v_0T} \lt x \lt {v_0T}.\) |
| 3. | the acceleration is always a non-negative number. |
| 4. | the motion has no turning points. |






