Q. No.The velocity-time \((v\text-t)\) graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in \(6\) s are, respectively:
1. \(8\) m, \(16\) m
2. \(16\) m, \(8\) m
3. \(16\) m, \(16\) m
4. \(8\) m, \(8\) m
2. \(16\) m, \(8\) m
3. \(16\) m, \(16\) m
4. \(8\) m, \(8\) m
In the following graph, the distance travelled by the body in metres is:
| 1. | \(200\) | 2. | \(250\) |
| 3. | \(300\) | 4. | \(400\) |
Which of the following velocity-time graphs shows a realistic situation for a body in motion?
| 1. |  |
2. |  |
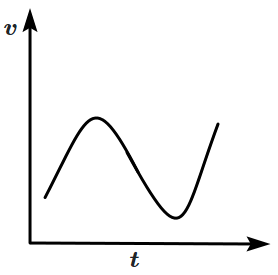| 3. |  |
4. |  |
Acceleration-time graph of a body is shown.
The corresponding velocity-time graph of the same body is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Given below are two statements:
| Assertion (A): | Position-time graph of a stationary object is a straight line parallel to the time axis. |
| Reason (R): | For a stationary object, the position does not change with time. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
The acceleration of a particle starting from rest varies with time according to the relation \(A= - a\omega^2\sin \omega t\). The displacement of this particle at a time \(t\) will be:
| 1. | \(-\frac{1}{2}\left(a\omega^2\sin\omega t\right)t^2\) | 2. | \(a\omega \sin \omega t\) |
| 3. | \(a\omega \cos \omega t\) | 4. | \(a\sin \omega t\) |
A thief is running away on a straight road in a jeep moving with a speed of \(9\) m/s. A policeman chases him on a motorcycle moving at a speed of \(10\) m/s. If the instantaneous separation of the jeep from the motorcycle is \(100\) m, how long will it take for the policeman to catch the thief?
1. \(1\) s
2. \(19\) s
3. \(90\) s
4. \(100\) s
A stone is dropped from a height \(h\). Simultaneously, another stone is thrown up from the ground which reaches a height \(4h\). The two stones cross each other after time:
1. \(\sqrt{\frac{h}{8g}}\)
2. \(\sqrt{8g}~h\)
3. \(\sqrt{2g}~h\)
4. \(\sqrt{\frac{h}{2g}}\)
Four marbles are dropped from the top of a tower one after the other at a one-second interval. The first one reaches the ground after \(4\) seconds. When the first one reaches the ground the distances between the first and second, the second and third, and the third and fourth will be, respectively:
| 1. | \(35\) m, \(25\) m, and \(15\) m | 2. | \(30\) m, \(20\) m, and \(10\) m |
| 3. | \(20\) m, \(10\) m, and \(5\) m | 4. | \(40\) m, \(30\) m, and \(20\) m |
© 2024 GoodEd Technologies Pvt. Ltd.