Q. No.The graph between the displacement \(x\) and time \(t\) for a particle moving in a straight line is shown in the figure.
During the interval OA, AB, BC and CD the acceleration of the particle is:
OA
AB
BC
CD
1.
+
0
+
+
2.
–
0
+
0
3.
+
0
–
+
4.
–
0
–
0
During the interval OA, AB, BC and CD the acceleration of the particle is:
A lift is going up. The variation in the speed of the lift is as given in the graph. What is the height to which the lift takes the passengers?
| 1. | \(3.6~\text{m}\) |
| 2. | \(28.8~\text{m}\) |
| 3. | \(36.0~\text{m}\) |
| 4. | It cannot be calculated from the above graph. |
The velocity-time \((v\text-t)\) graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in \(6\) s are, respectively:
1. \(8\) m, \(16\) m
2. \(16\) m, \(8\) m
3. \(16\) m, \(16\) m
4. \(8\) m, \(8\) m
In the following graph, the distance travelled by the body in metres is:
| 1. | \(200\) | 2. | \(250\) |
| 3. | \(300\) | 4. | \(400\) |
Which of the following velocity-time graphs shows a realistic situation for a body in motion?
| 1. |  |
2. |  |
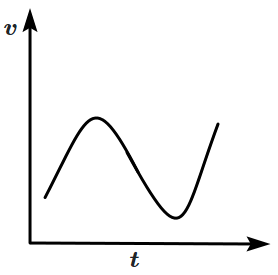| 3. |  |
4. |  |
Acceleration-time graph of a body is shown.
The corresponding velocity-time graph of the same body is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Given below are two statements:
| Assertion (A): | Position-time graph of a stationary object is a straight line parallel to the time axis. |
| Reason (R): | For a stationary object, the position does not change with time. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
The acceleration of a particle starting from rest varies with time according to the relation \(A= - a\omega^2\sin \omega t\). The displacement of this particle at a time \(t\) will be:
| 1. | \(-\frac{1}{2}\left(a\omega^2\sin\omega t\right)t^2\) | 2. | \(a\omega \sin \omega t\) |
| 3. | \(a\omega \cos \omega t\) | 4. | \(a\sin \omega t\) |
A thief is running away on a straight road in a jeep moving with a speed of \(9\) m/s. A policeman chases him on a motorcycle moving at a speed of \(10\) m/s. If the instantaneous separation of the jeep from the motorcycle is \(100\) m, how long will it take for the policeman to catch the thief?
1. \(1\) s
2. \(19\) s
3. \(90\) s
4. \(100\) s
© 2024 GoodEd Technologies Pvt. Ltd.