A particle is dropped vertically from rest from a height. The time taken by it to fall through successive distances of \(1~\text{m}\) each will then be:
1.
All equal, being equal to \(\sqrt{2 / g} \) s.
2.
In the ratio of the square roots of the integers \(1,2,3....\)
3.
In the ratio of the difference in the square roots of the integers \(\sqrt{1}\), \((\sqrt{2}-\sqrt{1})\),\((\sqrt{3}-\sqrt{2})\),\((\sqrt{4}-\sqrt{3})\) \( \ldots\)
4.
In the ratio of the reciprocal of the square roots of the integers i.e,... \(\frac{1}{\sqrt{1}}\), \(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{3}}\),\(\frac{1}{\sqrt{4}} \)
The graph between the displacement \(x\) and time \(t\) for a particle moving in a straight line is shown in the figure.
During the interval OA, AB, BC and CD the acceleration of the particle is:
| OA | AB | BC | CD | |
| 1. | + | 0 | + | + |
| 2. | – | 0 | + | 0 |
| 3. | + | 0 | – | + |
| 4. | – | 0 | – | 0 |
A lift is going up. The variation in the speed of the lift is as given in the graph. What is the height to which the lift takes the passengers?

| 1. | \(3.6~\text{m}\) |
| 2. | \(28.8~\text{m}\) |
| 3. | \(36.0~\text{m}\) |
| 4. | It cannot be calculated from the above graph. |
The velocity-time \((v\text-t)\) graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in \(6\) s are, respectively:

1. \(8\) m, \(16\) m
2. \(16\) m, \(8\) m
3. \(16\) m, \(16\) m
4. \(8\) m, \(8\) m
In the following graph, the distance travelled by the body in metres is:
| 1. | \(200\) | 2. | \(250\) |
| 3. | \(300\) | 4. | \(400\) |
Which graph represents a uniformly accelerated motion?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Which of the following velocity-time graphs shows a realistic situation for a body in motion?
| 1. |  |
2. | 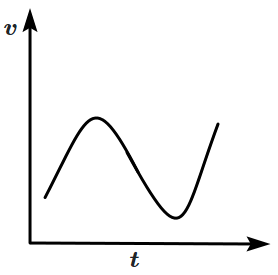 |
| 3. |  |
4. |  |
Acceleration-time graph of a body is shown.
The corresponding velocity-time graph of the same body is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Given below are two statements:
| Assertion (A): | Position-time graph of a stationary object is a straight line parallel to the time axis. |
| Reason (R): | For a stationary object, the position does not change with time. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
| 1. | \(-\frac{1}{2}\left(a\omega^2\sin\omega t\right)t^2\) | 2. | \(a\omega \sin \omega t\) |
| 3. | \(a\omega \cos \omega t\) | 4. | \(a\sin \omega t\) |









